陕西省渭南市大荔县2020-2021学年高一上学期数学期末考试试卷

试卷更新日期：2021-02-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {0, 1, 2}$ ， $B = {x | - 1 < x < 2}$ ，则 $A \cap B =$ （）

A、{0} B、{1} C、 ${0, 1}$ D、 ${0, 1, 2}$

查看试题解析
2. 在空间直角坐标系中，点 $(- 2, 1, 9)$ 关于 $x$ 轴的对称点的坐标是（）

A、 $(- 2, 1, 9)$ B、 $(- 2, - 1, - 9)$ C、 $(2, - 1, 9)$ D、 $(2, 1, - 9)$

查看试题解析
3. 下列四组函数中，表示同一函数的是（）.

A、 $y = x^{0}$ 与 $y = 1$ B、 $y = x$ 与 $y = \frac{x^{2}}{x}$ C、 $y = | x |$ 与 $y = {(\sqrt{x})}^{2}$ D、 $y = | x |$ 与 $y = \sqrt{x^{2}}$

查看试题解析
4. 如图， $Δ O^{'} A^{'} B^{'}$ 是水平放置的 $Δ O A B$ 的直观图， $O^{'} A^{'} = O^{'} B^{'} = 2$ ， $∠ A^{'} O^{'} B^{'} = 45^{\circ}$ ，则 $Δ O A B$ 的面积是（）

A、2 B、3 C、4 D、5

查看试题解析
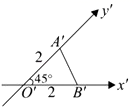5. 已知直线 $l_{1} : (3 + a) x + 4 y - 5 + 3 a = 0$ 与 $l_{2} : 2 x + (5 + a) y - 8 = 0$ 平行，则a等于（）.

A、-7或-1 B、7或1 C、-7 D、-1

查看试题解析
6. 函数 $y = \sqrt{\log_{\frac{1}{2}} (x - 1)}$ 的定义域为（）

A、 $(1 ， + \infty)$ B、 $[2 ， + \infty)$ C、 $(1 ， 2]$ D、 $[1 ， 2]$

查看试题解析
7. 已知某几何体的三视图如图所示（单位：cm），则该几何体的侧面积为（）

A、πcm² B、2πcm² C、4πcm² D、8πcm²

查看试题解析
8. 设 $a = \log_{\frac{1}{3}} 2$ ， $b = {(\frac{1}{3})}^{- 1.1}$ ， $c = {(\frac{1}{2})}^{0.3}$ ，则（）

A、 $a < b < c$ B、 $a < c < b$ C、 $b < c < a$ D、 $b < a < c$

查看试题解析
9. 直线 $x + y = 0$ 被圆 $x^{2} + y^{2} - 6 x + 2 y + 4 = 0$ 截得的弦长等于（）

A、4 B、2 C、 $2 \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
10. 设m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是（）

A、若 $α ⊥ γ$ ， $β ⊥ γ$ ，则 $α / / β$ B、若 $m ⊥ n$ ， $m ⊥ α$ ， $n / / β$ ，则 $α / / β$ C、若 $m ⊥ α$ ， $m ⊥ β$ ，则 $α / / β$ D、若 $m / / n$ ， $m / / α$ ， $n / / β$ ，则 $α / / β$

查看试题解析
11. 我国古代《九章算术》里，记载了一个“商功”的例子：今有刍童，下广二丈，袤三丈，上广三丈，袤四丈，高三丈.问积几何？其意思是：今有上下底面皆为长方形的草垛（如图所示），下底宽2丈，长3丈；上底宽3丈，长4丈；高3丈.问它的体积是多少？该书提供的算法是：上底长的2倍与下底长的和与上底宽相乘，同样下底长的2倍与上底长的和与下底宽相乘，将两次运算结果相加，再乘以高，最后除以6.则这个问题中的刍童的体积为（）

A、13.25立方丈 B、26.5立方丈 C、53立方丈 D、106立方丈

查看试题解析
12. 已知 $P$ 是直线 $l$ ： $k x + y + 4 = 0 (k > 0)$ 上一动点， $P A$ 、 $P A$ 是圆 $C$ ： $x^{2} + y^{2} - 2 y = 0$ 的两条切线，切点分别为 $A$ 、 $B$ ，若四边形 $P A C B$ 的最小面积为 $2$ ，则 $k =$ （）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{6}}{3}$ C、 $2$ D、 $4$

查看试题解析

二、填空题

13. 设函数 $f (x) = {\begin{matrix} x^{2} - 2^{x}, (x \leq 0) \\ f (x - 3), (x > 0) \end{matrix}$ ,则 $f (6)$ 的值为.

查看试题解析
14. 三条直线两两相交，它们可以确定的平面有个．

查看试题解析
15. 过直线 $x - 2 y + 4 = 0$ 和 $x + y - 2 = 0$ 的交点，且过点 $(2, - 1)$ 的直线 $l$ 的方程为．

查看试题解析
16. 魏晋时期数学家刘徽在他的著作《九章算术注》中，称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”（如图所示），刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为 $π ： 4$ ．若“牟合方盖”的体积为 $\frac{16}{3}$ ，则正方体的外接球的表面积为．

查看试题解析

三、解答题

17. 计算求值.

(1)、 ${(\sqrt[3]{2} \times \sqrt{3})}^{6} + {(\sqrt{2^{\frac{3}{2}}})}^{\frac{4}{3}} - {(- 2021)}^{0}$ ；

(2)、 $\log_{3} \sqrt[4]{27} + \lg 25 - 5^{\log_{5} \frac{7}{4}} + \lg 4$ .

查看试题解析
18. 已知点M(0，3)，N(-4，0)及点P(-2，4)；

(1)、若直线l经过点P且l $//$ MN，求直线l的方程；

(2)、求△MNP的面积.

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，四边形 $A B C D$ 是矩形，平面 $P C D ⊥$ 平面 $A B C D$ ， $M$ 为 $P C$ 中点.
（Ⅰ）求证： $P A / /$ 平面 $M D B$ ；

（Ⅱ） $P D ⊥ B C$ .

查看试题解析
20. 已知函数 $f (x) = e^{x} - e^{- x}$ .

(1)、判断函数 $f (x)$ 的奇偶性，并证明；

(2)、证明函数 $f (x)$ 在R上单调递增；

(3)、若 $f (1 - m) + f (2 m + 1) \leq 0$ ，求实数 $m$ 的取值范围.

查看试题解析
21. 据说伟大的阿基米德逝世后，敌军将领马塞拉斯给他建了一块墓碑，在墓碑上刻了一个如图所示的图案，图案中球的直径、圆柱底面的直径和圆柱的高相等，圆锥的顶点为圆柱上底面的圆心，圆锥的底面是圆柱的下底面．

(1)、试计算出图案中圆柱与球的体积比；

(2)、假设球半径 $r = 12 c m$ ．试计算出图案中圆锥的体积和表面积.

查看试题解析
22. 已知圆 $C$ 经过原点 $O (0, 0)$ 且与直线 $y = 2 x - 8$ 相切于点 $P (4, 0)$
（Ⅰ）求圆 $C$ 的方程；

（Ⅱ）在圆 $C$ 上是否存在两点 $M, N$ 关于直线 $y = k x - 1$ 对称，且以线段 $M N$ 为直径的圆经过原点？若存在,写出直线 $M N$ 的方程；若不存在，请说明理由

查看试题解析