初中数学苏科版九年级下册 5.5 用二次函数解决问题 同步训练
试卷更新日期：2021-02-22 类型：同步测试
一、单选题
-
1. 国家实施”精准扶贫“政策以来，很多贫困人口走向了致富的道路．某地区2016年底有贫困人口9万人，通过社会各界的努力，2018年底贫困人口减少至1万人．设2016年底至2018年底该地区贫困人口的年平均下降率为 ，根据题意列方程得（ ）A、 B、 C、 D、2. 服装店将进价为每件100元的服装按每件x（x＞100）元出售，每天可销售（200﹣x）件，若想获得最大利润，则x应定为（ ）A、150元 B、160元 C、170元 D、180元3.
如图，假设篱笆（虚线部分）的长度16m，则所围成矩形ABCD的最大面积是（ ）
A、60m2 B、63m2 C、64m2 D、66m24. 某公园有一个圆形喷水池，喷出的水流呈抛物线，一条水流的高度h（单位：m）与水流运动时间t（单位：s）之间的关系式为h=30t﹣5t2 ， 那么水流从抛出至回落到地面所需要的时间是（ ）A、6s B、4s C、3s D、2s5. 某旅游景点的收入受季节的影响较大，有时候出现赔本的经营状况.因此，公司规定：若无利润时，该景点关闭.经跟踪测算，该景点一年中的利润W（万元）与月份x之间满足二次函数W=﹣x2+16x﹣48，则该景点一年中处于关闭状态有（ ）月.A、5 B、6 C、7 D、86. 从地面竖直向上抛出一小球，小球的高度 h （单位： m ）与小球运动时间 （单位： s ）之间的函数关系如图所示．下列结论：①小球在空中经过的路程是 40m ；②小球运动的时间为 6s ；③小球抛出3秒时，速度为0；
④当 时，小球的高度 ．其中正确的是（ ）
A、①④ B、①② C、②③④ D、②④7. 如图，等腰Rt△ABC（∠ACB=90°）的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让△ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
A、
B、
C、
D、
8. 如图，某隧道美化施工，横截面形状为抛物线y =－ x2 + 8（单位：米），施工队计划在隧道正中搭建一个矩形脚手架DEFG，已知DE：EF = 3：2，则脚手架高DE为（ ）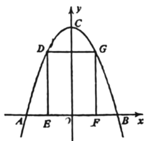
A、7米 B、6.3米 C、6米 D、5米9. 图2是图1中拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可近似看成抛物线y=﹣
（x﹣80）2+16，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴，若OA=10米，则桥面离水面的高度AC为（ ）
A、16
米
B、
米
C、16 
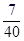米
D、
米
10. 某地要建造一个圆形喷水池，在水池中央垂直于地面安装一个柱子OA，O恰为水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上，建立平面直角坐标系（如图），水流喷出的高度y（m）与水平距离x（m）之间的关系式是 ，则下列结论：（1）柱子OA的高度为3m；（2）喷出的水流距柱子1m处达到最大高度；（3）喷出的水流距水平面的最大高度是4m；（4）水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有（ ）
A、1个 B、2个 C、3个 D、4二、填空题
-
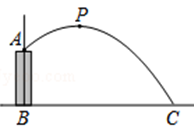
11. 小明推铅球，铅球行进高度 与水平距离 之间的关系为 ，则小明推球的成绩是m.12. 把一个小球以20米/秒的速度竖直向上弹出，它在空中的高度h（米）与时间t（秒），满足关系：h=20t-5t2 ， 当小球达到最高点时，小球的运动时间为第秒时．13. 如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2m，喷出水流的运动路线是抛物线，如果水流的最高点P到喷水枪AB所在直线的距离为2m，且到地面的距离为3m，则水流的落地点C到水枪底部B的距离为.
14. 某电商销售一款夏季时装，进价40元/件，售价110元/件，每天销售20件，每销售一件需缴纳电商平台推广费用a元（a＞0）．未来30天，这款时装将开展“每天降价1元”的夏令促销活动，即从第1天起每天的单价均比前一天降1元．通过市场调研发现，该时装单价每降1元，每天销量增加4件．在这30天内，要使每天缴纳电商平台推广费用后的利润随天数t（t为正整数）的增大而增大，a的取值范围应为 ．
15. 如图，有一个横截面边缘为抛物线的隧道入口，隧道入口处的底面宽度为 ，两侧距底面 高处各有一盏灯，两灯间的水平距离为 ，则这个隧道入口的最大高度为 .
16. 一养鸡专业户计划用116m长的篱笆围成如图所示的三间长方形鸡舍，门MN宽2m，门PQ和RS的宽都是1m，围成的鸡舍面积最大是平方米.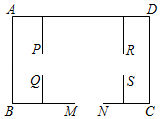
17. 如图，一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系，跨度AB=44米，∠A=45°，AC1=4米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH=米.
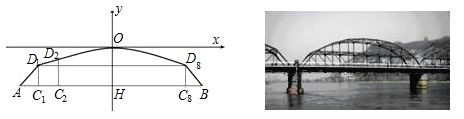18.闵行体育公园的圆形喷水池的水柱（如图1）如果曲线APB表示落点B离点O最远的一条水流（如图2），其上的水珠的高度）y（米）关于水平距离x（米）的函数解析式为y=﹣x2+4x+ ， 那么圆形水池的半径至少为 米时，才能使喷出的水流不落在水池外．
三、综合题
-
19. 如图，一块草地是长80 m，宽60 m的矩形，欲在中间修筑两条互相垂直的宽为xm的小路，这时草坪面积为y m2 ． 求y与x的函数关系式，并写出自变量x的取值．
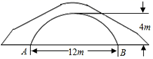
20. 如图所示的是一座拱桥，桥洞的拱形是抛物线的形状，当水面宽AB为12米时，桥洞顶部离水面4米，若水面上涨1米，求此时水面的宽．
21. 某商场要经营一种新上市的文具，进价为20元/件，试营销阶段发现，当销售单价是25 元时，每天的销 售量为 250 件；销售单价每上涨1元，每天的销售量就减少10件．(1)、写出商场销售这种文具每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；(2)、商场的营销部结合上述情况，提出了A、B两种营销方案：方案A：该文具的销售单价高于进价且不超过30元；方案B：每天销售量不少于10件，且每件文具的利润至少为25元．请比较哪种方案的最大利润更高，并说明理由．22. 某商场将进价40元一个的某种商品按50元一个售出时，每月能卖出500个，商场想了两个方案来增加利润:方案一提高价格，但这种商品每个售价涨价1元，销售量就减少10个；
方案二:售价不变，但发资料做广告，已知这种商品每月的广告费用m（千元）与销售量倍数p关系为p=-0.4m2+2m，
试通过计算，请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由.
23. 某服装厂生产A品种服装，每件成本为71元，零售商到此服装厂一次性批发A品牌服装x件时，批发单价为y元，y与x之间满足如下图所示的函数关系，其中批发件数x为10的正整数倍.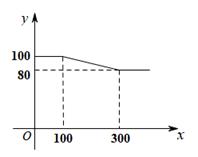
(1)、当100≤x≤300 时，则y与x的函数关系式为；(2)、某零售商到此服装厂一次性批发A品牌服装200件，需要支付元；(3)、若零售商到此服装厂一次性批发A品牌服装x(100≤x≤400) 件，服装厂的利润为w元，求：x 为何值时，w最大？最大值是多少？24. “扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量 （件）与销售单价 （元）之间存在一次函数关系，如图所示.
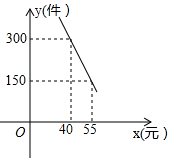(1)、求 与 之间的函数关系式；(2)、如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？(3)、该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.25. 某商店销售一种进价50元/件的商品，经市场调查发现：该商品的每天销售量y（件）是售价x（元/件）的一次函数，其售价、销售量的二组对应值如下表：售价x（元/件）
55
65
销售量y（件/天）
90
70
(1)、若某天销售利润为800元，求该天的售价为多少元/件.(2)、由于某种原因，该商品进价提高了a元/件（a＞0），商店售价不低于进价，物价部门规定该商品售价不得超过70元件，该商店在今后的销售中，每天能获得的销售最大利润是960元，求a的值.26. 如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y= x2- x+3的绳子．
(1)、求绳子最低点离地面的距离；(2)、因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子(如图2)，使左边抛物线F1的最低点距MN为1米，离地面1.8米．求MN的长；(3)、将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为 ，设MN离AB的距离为m，抛物线F2的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．