初中数学苏科版九年级下册 5.4 二次函数与一元二次方程 同步训练
试卷更新日期:2021-02-20 类型:同步测试
一、单选题
-
1. 二次函数y=x2﹣2x﹣3图象与y轴的交点坐标是( )A、(0,1) B、(1,0) C、(-3,0) D、(0,-3)2. 抛物线y=-3x2+2x-1的图象与坐标轴的交点个数是 ( )A、无交点 B、1个 C、2个 D、3个3. 已知二次函数 图象上部分点的坐标 的对应值如表所示:
x
…
0
4
…
y
…
0.37
-1
0.37
…
则方程 的根是( ).
A、0或4 B、 或 C、 或 D、无实根4. 根据表格中的数据,估计一元二次方程 ( , , 为常数, )一个解 的范围为( )0.5
1
1.5
2
3
28
18
10
4
-2
A、 B、 C、 D、5. 如图,抛物线 与直线 交于点 , ,则不等式 的解集为( )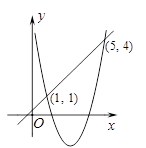 A、 B、 或 C、 D、 或6. 若函数 的图象与坐标轴有三个交点,则b的取值范围是
A、 B、 或 C、 D、 或6. 若函数 的图象与坐标轴有三个交点,则b的取值范围是 A、 且 B、 C、 D、7. 某旅游景点的收入受季节的影响较大,有时候会出现赔本经营的状况。因此,公司规定,若无利润时该景点关闭。经跟踪测算,该景点一年中的月利润
A、 且 B、 C、 D、7. 某旅游景点的收入受季节的影响较大,有时候会出现赔本经营的状况。因此,公司规定,若无利润时该景点关闭。经跟踪测算,该景点一年中的月利润 (万元)与月份x满足 ,则该景点一年中处于关闭状态的时长为( ) A、5个月 B、6个月 C、7个月 D、8个月8. 已知二次函数 的图象经过 与 两点,关于x的方程 有两个根,其中一个根是3.则关于x的方程 有两个整数根,这两个整数根是( )A、-2或0 B、-4或2 C、-5或3 D、-6或49. 抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1 , 0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是( )A、方程ax2+bx+c=2的一个根是x=﹣2 B、若x1=2,则抛物线与x轴的另一个交点为(﹣4,0) C、若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2 D、若 ≤x≤0时,2≤y≤3,则a=10. 如图是抛物线 的部分图象,其对称轴为直线 ,与 轴的交点坐标为 ,下列结论:① ;② ;③方程 的两根分别是0和2;④方程 有一个实根大于2;⑤当 时, 随着 的增大而减小. 其中正确结论的个数是( )
(万元)与月份x满足 ,则该景点一年中处于关闭状态的时长为( ) A、5个月 B、6个月 C、7个月 D、8个月8. 已知二次函数 的图象经过 与 两点,关于x的方程 有两个根,其中一个根是3.则关于x的方程 有两个整数根,这两个整数根是( )A、-2或0 B、-4或2 C、-5或3 D、-6或49. 抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1 , 0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是( )A、方程ax2+bx+c=2的一个根是x=﹣2 B、若x1=2,则抛物线与x轴的另一个交点为(﹣4,0) C、若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2 D、若 ≤x≤0时,2≤y≤3,则a=10. 如图是抛物线 的部分图象,其对称轴为直线 ,与 轴的交点坐标为 ,下列结论:① ;② ;③方程 的两根分别是0和2;④方程 有一个实根大于2;⑤当 时, 随着 的增大而减小. 其中正确结论的个数是( )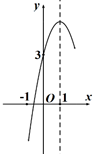 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
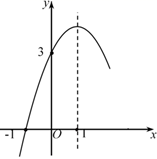
11. 抛物线 与 轴交于两点,分别是 , ,则 .12. 已知关于 的一元二次方程 的一个根是 ,且二次函数 的对称轴是直线 ,则此方程 的另一个解为.13. 二次函数 的部分图象如图所示,对称轴为直线 ,则关于x的方程 的解为.
 14. 二次函数y=x2+(k+4)x+k的图象与x轴两个交点间的最短距离为。15. 在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:
14. 二次函数y=x2+(k+4)x+k的图象与x轴两个交点间的最短距离为。15. 在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:…
1
2
3
4
5
6
7
8
…
…
-1.78
-3.70
-4.42
-3.91
-2.20
4.88
10.27
…
根据以上信息,关于 的一元二次方程 的两个实数根中,其中的一个实数根约等于(结果保留小数点后一位).
16. 如图,已知函数 与 的图象交于A(-4,1)、B(2,-2) 、C(1,-4)三点,根据图象可求得关于x的不等式 的解集为.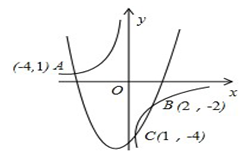 17. 若二次函数 ( 为常数)的图象在 的部分与 轴有两个公共点,则 的取值范围是.18. 抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是 .
17. 若二次函数 ( 为常数)的图象在 的部分与 轴有两个公共点,则 的取值范围是.18. 抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是 .三、综合题
-
19. 已知二次函数 .求证:不论 为何实数,此二次函数的图象与 轴都有两个不同交点.20. 已知关于x的二次函数 .(1)、试判断该函数的图象与x轴的交点的个数;(2)、当 时,求该函数图象与x轴的两个交点之间的距离.21. 已知二次函数 (m是常数)(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿x轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?22. 已知抛物线为: .(1)、若该抛物线与y轴交于 ,与 轴仅有一个交点,求抛物线的解析式;(2)、若该抛物线的开口向下, , 是抛物线上的两点,当 时,直接写出 的取值范围.23. 已知抛物线y=x2+bx+c的图象如图所示,它与x轴的一个交点的坐标为A(﹣1,0),与y轴的交点坐标为C(0,﹣3).
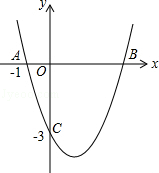 (1)、求抛物线的解析式及与x轴的另一个交点B的坐标;(2)、根据图象回答:当x取何值时,y<0?(3)、在抛物线的对称轴上有一动点P,求PA+PB的值最小时的点P的坐标.24. 已知二次函数 ( 为常数).(1)、当 时,求二次函数的最值;(2)、当抛物线的顶点恰好落在 轴上时,求抛物线的顶点坐标;(3)、当 时,与其对应的函数值 的最大值为2,求二次函数的解析式.25. 已知:二次函数 .
(1)、求抛物线的解析式及与x轴的另一个交点B的坐标;(2)、根据图象回答:当x取何值时,y<0?(3)、在抛物线的对称轴上有一动点P,求PA+PB的值最小时的点P的坐标.24. 已知二次函数 ( 为常数).(1)、当 时,求二次函数的最值;(2)、当抛物线的顶点恰好落在 轴上时,求抛物线的顶点坐标;(3)、当 时,与其对应的函数值 的最大值为2,求二次函数的解析式.25. 已知:二次函数 .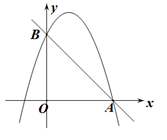 (1)、如果二次函数图象与x轴有两个交点,求m的取值范围;(2)、如图,二次函数的图象过点A(3,0),与y轴交于点B , 求直线AB解析式.26. 如图,抛物线y=- x2+ x+2与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)、如果二次函数图象与x轴有两个交点,求m的取值范围;(2)、如图,二次函数的图象过点A(3,0),与y轴交于点B , 求直线AB解析式.26. 如图,抛物线y=- x2+ x+2与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
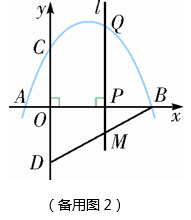 (1)、求点A,点B,点C的坐标.(2)、求直线BD的表达式.(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形.(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求点A,点B,点C的坐标.(2)、求直线BD的表达式.(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形.(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.