陕西省安康市紫阳县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-20 类型:期末考试
一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的,请将正确答案的序号填在题前的答题栏中)
-
1. 下列事件中,是必然事件的是( )A、一名运动员跳高的最好成绩是20.1米 B、一人买一张火车票,座位刚好靠窗口 C、通常加热到100℃时,水沸腾 D、购买一张彩票,中奖2. 下列图形中,是中心对称图形的是( )A、
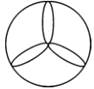 B、
B、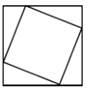 C、
C、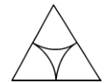 D、
D、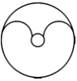 3. 一个不透明的袋子装有除颜色外其余均相同的2个红球和m个黄球,随机从袋中摸出一个球记录下颜色,再放回袋中摇匀.大量重复试验后,发现摸出红球的频率稳定在0.2附近,则m的值为( )A、8 B、10 C、6 D、44. 若关于x的方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 D、5. 如图,将 绕点A顺时针旋转到 的位置,且点D恰好在AC边上,则下列结论不一定成立的是( )
3. 一个不透明的袋子装有除颜色外其余均相同的2个红球和m个黄球,随机从袋中摸出一个球记录下颜色,再放回袋中摇匀.大量重复试验后,发现摸出红球的频率稳定在0.2附近,则m的值为( )A、8 B、10 C、6 D、44. 若关于x的方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 D、5. 如图,将 绕点A顺时针旋转到 的位置,且点D恰好在AC边上,则下列结论不一定成立的是( )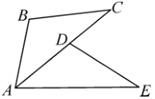 A、 B、 C、AC平分 D、6. 如图,函数 与 在同一平面直角坐标系中的大致图象是( )A、
A、 B、 C、AC平分 D、6. 如图,函数 与 在同一平面直角坐标系中的大致图象是( )A、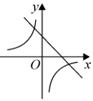 B、
B、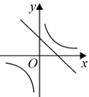 C、
C、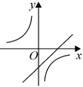 D、
D、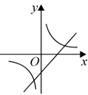 7. 有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机的放入其中两个信封里,则信封与信编号都相同的概率为( )A、 B、 C、 D、8. 由于疫情得到缓和,餐饮行业逐渐回暖,某家餐厅重新开张,开业第一天收入约为3020元,之后两天的收入按相同的增长率增长,第三天收入约为4350元.设每天的增长率为x,根据题意可列方程为( )A、 B、 C、 D、9. 如图,AB为 的直径,点C,点D是 上的两点,连接CA,CD,AD.若 ,则 的度数是( )
7. 有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机的放入其中两个信封里,则信封与信编号都相同的概率为( )A、 B、 C、 D、8. 由于疫情得到缓和,餐饮行业逐渐回暖,某家餐厅重新开张,开业第一天收入约为3020元,之后两天的收入按相同的增长率增长,第三天收入约为4350元.设每天的增长率为x,根据题意可列方程为( )A、 B、 C、 D、9. 如图,AB为 的直径,点C,点D是 上的两点,连接CA,CD,AD.若 ,则 的度数是( ) A、110° B、120° C、130° D、140°10. 若抛物线 与x轴两个交点间的距离为4,称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向上平移3个单位,得到的新抛物线经过点( )A、 B、 C、 D、
A、110° B、120° C、130° D、140°10. 若抛物线 与x轴两个交点间的距离为4,称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向上平移3个单位,得到的新抛物线经过点( )A、 B、 C、 D、二、填空题(共4小题,每小题3分,计12分)
-
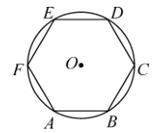
11. 一元二次方程 的解是.12. 如图,正六边形ABCDEF内接于 ,若 ,则 的半径为.
 13. 如图,反比例函数 的图象经过 的顶点A,点C在x轴上, 轴.若点B的坐标为 , ,则k的值为.
13. 如图,反比例函数 的图象经过 的顶点A,点C在x轴上, 轴.若点B的坐标为 , ,则k的值为. 14. 如图,在正方形ABCD中, ,点E在CD边上,且 ,将 绕点A顺时针旋转90°,得到 ,连接 ,则线段 的长为.
14. 如图,在正方形ABCD中, ,点E在CD边上,且 ,将 绕点A顺时针旋转90°,得到 ,连接 ,则线段 的长为.
三、解答题(共11小题,计78分,解答应写出过程)
-
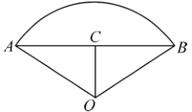
15. 解方程: .16. 如图, 的半径 , 于点C, .求 的长.
 17. 如图,在 中, ,请用尺规作图法求作 的外接圆 .(保留作图痕迹,不写作法)
17. 如图,在 中, ,请用尺规作图法求作 的外接圆 .(保留作图痕迹,不写作法) 18. 如图, 的顶点坐标分别为 , , .画出 绕原点O逆时针旋转90°后得到的 ,并写出点 的坐标.
18. 如图, 的顶点坐标分别为 , , .画出 绕原点O逆时针旋转90°后得到的 ,并写出点 的坐标. 19. 已知关于x的一元二次方程 .(1)、若 是该方程的一个根,求k的值;(2)、请判定这个方程根的情况.20. 如图,在一块长为16m,宽为10m的矩形空地中,修建2条同样宽的小路(图中阴影部分),剩下的部分种植草坪,要使草坪的面积为 ,求道路的宽度.
19. 已知关于x的一元二次方程 .(1)、若 是该方程的一个根,求k的值;(2)、请判定这个方程根的情况.20. 如图,在一块长为16m,宽为10m的矩形空地中,修建2条同样宽的小路(图中阴影部分),剩下的部分种植草坪,要使草坪的面积为 ,求道路的宽度.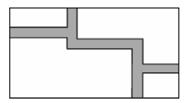 21. 元旦晚会上,甲、乙、丙、丁四个同学玩“击鼓传花”的游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.(1)、甲第一次传花时,求恰好传给乙的概率;(2)、请用画树状图或列表法求经过两次传花后,花恰好回到甲手中的概率.22. 如图,反比例函数 与直线 相交于A,B两点,过点A作 轴,垂足为点C,且 .
21. 元旦晚会上,甲、乙、丙、丁四个同学玩“击鼓传花”的游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.(1)、甲第一次传花时,求恰好传给乙的概率;(2)、请用画树状图或列表法求经过两次传花后,花恰好回到甲手中的概率.22. 如图,反比例函数 与直线 相交于A,B两点,过点A作 轴,垂足为点C,且 . (1)、求反比例函数的表达式及点B的坐标;(2)、观察图象,求出不等式 的解集.23. 如图,在 中,AB为直径,CD与 相切于点C,弦 于点E,连接AC.
(1)、求反比例函数的表达式及点B的坐标;(2)、观察图象,求出不等式 的解集.23. 如图,在 中,AB为直径,CD与 相切于点C,弦 于点E,连接AC.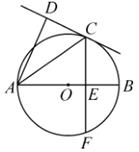 (1)、求证: ;(2)、当 时, , ,求AD的长.24. 如图,抛物线 经过x轴上 , 两点,且与y轴交于点C,抛物线的对称轴DE交x轴于点E,点D是其顶点,连接BD.
(1)、求证: ;(2)、当 时, , ,求AD的长.24. 如图,抛物线 经过x轴上 , 两点,且与y轴交于点C,抛物线的对称轴DE交x轴于点E,点D是其顶点,连接BD. (1)、求该抛物线的函数表达式;(2)、在抛物线的对称轴上是否存在点Q,使得 是以BC为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.25. 如图①,在 中,点D,E分别在AB,AC上,且 , .
(1)、求该抛物线的函数表达式;(2)、在抛物线的对称轴上是否存在点Q,使得 是以BC为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.25. 如图①,在 中,点D,E分别在AB,AC上,且 , . (1)、求证: ;(2)、若 ,把 绕点A逆时针旋转到图②的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
(1)、求证: ;(2)、若 ,把 绕点A逆时针旋转到图②的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.①试判断 的形状,并说明理由;
②将 绕点A在平面内自由旋转,若 , ,则 面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.