浙江省嘉兴市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-02-20 类型：期末考试

进入出卷网下载

一、选择题（每小题有4个选项，其中有且只有一个正确.每小题3分，共30分）

1. 已知 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{a-b}{b}$ 的值是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列事件中，属于不可能事件的是（）

A、打开电视机，正在播放天气预报 B、在一个只装有红球的袋子里摸出黑球 C、今年的除夕夜会下雪 D、任意抛掷一枚硬币8次，正面朝上有4次

查看试题解析
3. 正六边形的一个内角的度数是（）

A、60° B、 90° C、 120° D、150°

查看试题解析
4. 二次函数 y = x²+2x-1的图象与y轴的交点坐标是（）

A、（-2，0） B、（0，-2） C、（-1，0） D、（0，-1 ）

查看试题解析
5. 若扇形的半径为3，圆心角为60°，则此扇形的弧长是（）

A、π B、 2π C、 3π D、4π

查看试题解析
6. 如图，△如C中，点D，E分别在边AB，AC上.若 $\frac{A D}{A C} = \frac{A E}{A B} = \frac{2}{3}$ ，BC=2，则DE的长为（）

A、 $\frac{1}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、3

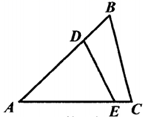查看试题解析
7. 如图，转盘中点A，B，C在圆上，∠4=40°，∠B=60° ，让转盘绕圆心O自由转动，当转盘停止时指针指向区域III的概率是（）

A、 $\frac{2}{9}$ B、 $\frac{1}{3}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

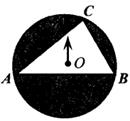查看试题解析
8. 二次函数y = ax²-2x-3（a<0）的图象一定不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 如图，A，B，C是直角坐标系中的三个点，现以坐标原点O为位似中心，作与△ABC的位似比为 $\frac{1}{2}$ 的位似图形△A'B'C'.若点A的坐标为（-1，1），则点 A'的坐标为（）

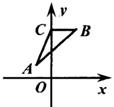A、（ $\frac{1}{2}$ ， $\frac{1}{2}$ ） B、（ $- \frac{1}{2}$ ， $\frac{1}{2}$ ）或（ $\frac{1}{2}$ ，- $\frac{1}{2}$ ） C、（ $\frac{1}{2}$ ，- $\frac{1}{2}$ ） D、（ $\frac{1}{2}$ ， $\frac{1}{2}$ ）或（ - $\frac{1}{2}$ ，- $\frac{1}{2}$ ）

查看试题解析
10. 如图，△ABC中，∠ABC=90°，点E在CB的延长线上，BE= $\frac{1}{3}$ AB，过点E作ED⊥AC于D.若 AD=ED，AC=6，则CD的长为（）

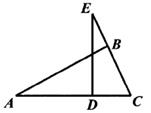A、1.5 B、2 C、2.5 D、4

查看试题解析

二、填空题（本题有10小题，每小题3分，共30分）

11. 已知△ABC∽△DEF，相似比为2，则它们的周长之比是.

查看试题解析
12. 任意写出一个正数和一个负数，两数之积是负数的概率是.

查看试题解析
13. 如图，四边形ABCD是⨀O的内接四边形.若∠A=50°，则∠BCD的度数是.

查看试题解析
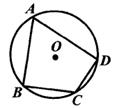14. 已知点P是线段AB的黄金分割点，AP>PB，若AB = 2，则AP的长为.

查看试题解析
15. 将抛物线y = x²先向右平移1个单位，再向上平移2个单位后，所得抛物线的函数表达式是.

查看试题解析
16. 如图，△ABC中，点D，E分别在边AB，AC上，请添加一个条件，使得△ADE与△ABC相似.

查看试题解析
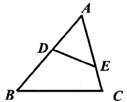17. 已知点 P （x₁ ， y₁ ）， Q （x₂ ， y₂）都在抛物线 y = x²-4x + 4上，若 x₁ + x₂ = 4，则y₁ y₂ .（填“>"、“<"或“=”）

查看试题解析
18. 将五个边长为2的正方形按如图所示放置，若A， B， C， D四点恰好在圆上，则这个圆的面积为 .（结果保留π）

查看试题解析
19. 将矩形纸片ABCD （如图1）折叠，使AB落在AD边上，折痕为AE（如图2），再将△AEB以BE为折痕向右折叠，AE与DC交于点F （如图3）.若S_△ADF= S_{四边形BDFE} ，则图1中 $\frac{AD}{A B}$ 的值为 .

查看试题解析
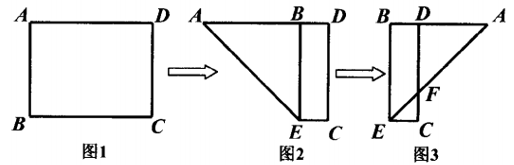20. 已知抛物线y = ax²+bx-2 （a≠0）的顶点在第三象限，且过点（1， 0），若a-b的值为整数，则b的值为 .

查看试题解析

三、解答题（第21〜24题，每题6分，第25、26题，每题8分，共40分）

21. 已知抛物线 y = x² +bx + c 经过点（-1， 0），（3， 0）.

(1)、求该抛物线的对称轴.

(2)、自变量x在什么范围内时，y随x的增大而减小？

查看试题解析

22. 对一批衬衣进行抽检，统计合格衬衣的件数，获得如下频数表.

抽取件数（件）	100	150	200	500	800	1000
合格频数	88	141	176	445	720	900
合格频率	______	0.94	0.88	0.89	0.90	______

(1)、完成上表.

(2)、估计任意抽一件衬衣是合格品的概率.

(3)、估计出售1200件衬衣，其中次品大约有几件.

查看试题解析

23. 如图，一组等距的平行线上有一个半圆，点O为圆心，AB为直径，点A，B，C，D是半圆弧与平行线的交点.只用无刻度的直尺作图.（保留作图痕迹）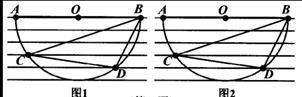

(1)、在图1中作出BD边上的中线CE.

(2)、在图2中作∠BCD的角平分线CF.

查看试题解析
24. 如图，△ABC绕点A按逆时针方向旋转100°得到△AEF.

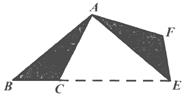(1)、当点E恰好落在BC延长线上时，求∠FEB的度数.

(2)、在（1）的条件下连结CF交AE于点D.
求证：AC² =AD·AE .

查看试题解析
25. 如图，在直角坐标系中，点A（0， 8），点B是x轴负半轴上的动点，以OA为直径作圆交AB于点D.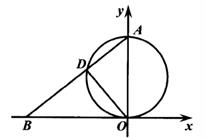

(1)、求证：∠AOD = ∠ABO.

(2)、当 ∠ABO = 30°时，求点D到y轴的距离.

(3)、求 $\frac{O D}{A B}$ 的最大值.

查看试题解析
26. 女生排球考试要求：垫球后，球在运动中离地面的最大高度至少为2米.某次模拟测试中，某女生在O处将球垫偏，之后又在A， B两处先后垫球，球沿抛物线C₁ → C₂ → C₃运动（假设抛物线C₁ ， C₂ ， C₃在同一平面内），最终正好在O处垫住，O处离地面的距离为1米.如图所示，以O为坐标原点1米为单位长度建立直角坐标系，x轴平行于地面水平直线m，已知点A（ $\frac{3}{2}$ ， $\frac{3}{8}$ ），点B的横坐标为 - $\frac{3}{2}$ ，抛物线C₁和C₃的表达式分别为 y = ax²- 2ax 和 y = 2ax² + bx （a≠ 0）.

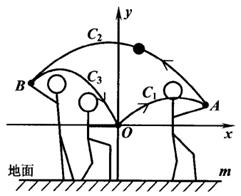(1)、求抛物线C₁的函数表达式.

(2)、第一次垫球后，球在运动中离地面的最大高度是否达到要求？请说明理由.

(3)、为了使第三次垫球后，球在运动中离地面的最大高度达到要求，该女生第三次垫球处B 离地面的高度至少为多少米？

查看试题解析