陕西省西安市莲湖区2020-2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-20 类型:期末考试
一、选择题(共10小题,每小题3分,计30分)
-
1. 下列函数是y关于x的反比例函数的是( )A、y= B、y= C、y=﹣ D、y=﹣2. 若△ABC∼△DEF,相似比为3:2,则△ABC与△DEF的面积比为( )A、3:2 B、9:4 C、2:3 D、4:93. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8km,则M,C两点间的距离为( )
 A、1.2 km B、2.4 km C、3.6 km D、4. 8 km4. 如图所示的物体的左视图是( )
A、1.2 km B、2.4 km C、3.6 km D、4. 8 km4. 如图所示的物体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在△ABC中,DE∥AB,且 ,则 的值为( )
5. 如图,在△ABC中,DE∥AB,且 ,则 的值为( ) A、 B、 C、 D、6. 某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为( )A、 B、 C、 D、7. 如图,A是反比例函数y= (x>0)的图象上的一点,过点A作AB⊥x轴,垂足为B.C为y轴上的一点,连接AC,BC则△ABC的面积为( )
A、 B、 C、 D、6. 某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为( )A、 B、 C、 D、7. 如图,A是反比例函数y= (x>0)的图象上的一点,过点A作AB⊥x轴,垂足为B.C为y轴上的一点,连接AC,BC则△ABC的面积为( ) A、 B、3 C、5 D、108. 已知关于x的方程ax2+(1﹣a)x﹣1=0,下列结论正确的是( )A、当a=0时,方程无实数根 B、当a=﹣1时,方程只有一个实数根 C、当a=1时,有两个不相等的实数根 D、当a≠0时,方程有两个相等的实数根9. 关于反比例函数y= ,下列说法不正确的是( )A、函数图象分别位于第一、第三象限 B、函数图象关于原点中心对称 C、当x>0时,y随x的增大而增大 D、当﹣8<x<﹣1时,﹣8<y<﹣110. 如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
A、 B、3 C、5 D、108. 已知关于x的方程ax2+(1﹣a)x﹣1=0,下列结论正确的是( )A、当a=0时,方程无实数根 B、当a=﹣1时,方程只有一个实数根 C、当a=1时,有两个不相等的实数根 D、当a≠0时,方程有两个相等的实数根9. 关于反比例函数y= ,下列说法不正确的是( )A、函数图象分别位于第一、第三象限 B、函数图象关于原点中心对称 C、当x>0时,y随x的增大而增大 D、当﹣8<x<﹣1时,﹣8<y<﹣110. 如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )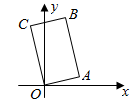 A、 B、3 C、 D、5
A、 B、3 C、 D、5二、填空题(共4小题,每小题3分,计12分)
-
11. 已知反比例函数的图象经过点(1,﹣2),那么这个反比例函数的解析式是.12. 如图,直线l1∥l2∥l3∥l4∥l5∥l6∥l7 , 且每相邻两条直线的距离相等.若直线l8分别与l1 , l2 , l5 , l7相交于点A,B,C,D,则AB:BC:CD为.
 13. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为.
13. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为.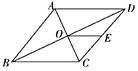 14. 如图,在正方形ABCD中,E是边BC的中点,连接AE,作EF⊥AE交正方形的外角平分线于点F,连接AF,交CD于点H,连接EH.若AB=4,则EH的长为.
14. 如图,在正方形ABCD中,E是边BC的中点,连接AE,作EF⊥AE交正方形的外角平分线于点F,连接AF,交CD于点H,连接EH.若AB=4,则EH的长为.
三、解答题(共11小题,计78分解答应写出过程)
-
15. 解方程:x2+4x﹣21=0.16. 若A(3,2)与B(1,a)是反比例函数y= (k≠0)图象上的点,求a的值.17. 如图,在△ABC中,AD是角平分线,请用尺规作图法,求作△ADE,使得△ABD∼△ADE,且点D与E对应,点E在AC上.(保留作图痕迹,不写作法)
 18. 如图,在△ABC中AC=BC,D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
18. 如图,在△ABC中AC=BC,D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形. 19. 如图所示是测量河宽的示意图,AE与BC相交于点D,AB⊥BC于点B,CE⊥BC于点C,测得BD=150m,DC=75m,EC=60m,求河宽AB.
19. 如图所示是测量河宽的示意图,AE与BC相交于点D,AB⊥BC于点B,CE⊥BC于点C,测得BD=150m,DC=75m,EC=60m,求河宽AB.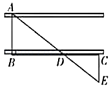 20. 2020年6月1日克强总理称赞地摊经济、小店经济是人间的烟火,是中国的生机.一时间,祖国大地上掀起了一股地摊经济的热潮.根据城管部门统一规划,甲,乙两兄弟只能从A,B,C,D四个街道中各随机选取一个街道摆地摊.(1)、“甲,乙两兄弟都到E街道摆地摊”是事件.(填“必然”,“不可能”或“随机”)(2)、试用画树状图或列表的方法求甲,乙两兄弟选在同一个街道摆地摊的概率.
20. 2020年6月1日克强总理称赞地摊经济、小店经济是人间的烟火,是中国的生机.一时间,祖国大地上掀起了一股地摊经济的热潮.根据城管部门统一规划,甲,乙两兄弟只能从A,B,C,D四个街道中各随机选取一个街道摆地摊.(1)、“甲,乙两兄弟都到E街道摆地摊”是事件.(填“必然”,“不可能”或“随机”)(2)、试用画树状图或列表的方法求甲,乙两兄弟选在同一个街道摆地摊的概率.
21. 如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于A(m,8),B(4,n)两点,连接OA,OB. (1)、求一次函数的表达式;
(1)、求一次函数的表达式;
(2)、求△AOB的面积.
22. 如图,在正方形ABCD中,E是BC的中点,点P在BC的延长线上,AP,DE交于点G,AP,CD交于点F. (1)、求证:AD•CF=CP•DF.
(1)、求证:AD•CF=CP•DF.
(2)、若DF=2CF,AB=6,求DG的长.
23. 某商店销售一款工艺品,每件的成本是30元,为了合理定价投放市场进行试销:据市场调查,销售单价是40元时,每天的销售量是80件,而销售单价每提高1元,每天就少售出2件,但要求销售单价不得超过55元.(1)、若销售单价为每件45元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1200元,那么每件工艺品售价应为多少元?24. 如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q连接CQ,∠BPC=∠AQP. (1)、求证:四边形ABCD是矩形;
(1)、求证:四边形ABCD是矩形;
(2)、当AP=3,AD=9时,求AQ和CQ的长.
25. 问题提出:如图,在锐角△ABC中,如何作一个正方形DEFG,使D,E落在BC边上,F,G分别落在AC,AB边上?勤奋小组同学给出了如下作法:①画一个有三个顶点落在△ABC两边上的正方形HIJK;②连接BJ,并延长交AC于点F;③过点F作EF⊥BC于点E;④过F作FG∥BC,交AB于点G;⑤过点G作GD⊥BC于点D,则四边形DEFG即为所求作的正方形.
受勤奋小组同学的启发,创新小组同学认为可以在锐角△ABC中,作出长与宽的比为2:1的矩形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.
 (1)、你认为勤奋小组同学的作法正确吗?请说明理由;(2)、请你帮助创新小组同学在在锐角△ABC中,作出所有满足长与宽的比为2:1的矩形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.(在备用图中完成,不写作法,保留作图痕迹)
(1)、你认为勤奋小组同学的作法正确吗?请说明理由;(2)、请你帮助创新小组同学在在锐角△ABC中,作出所有满足长与宽的比为2:1的矩形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.(在备用图中完成,不写作法,保留作图痕迹)
(3)、解决问题:
在(2)的条件下,已知△ABC的面积为36,BC=12,求出矩形DEFG的面积.