浙江省台州市黄路三区2021届九年级上学期数学期末联考试卷
试卷更新日期:2021-02-20 类型:期末考试
一、选择题(共10小题)
-
1. 下列事件是必然事件的是( )A、明天会下雨 B、某人骑车经过十字路口时遇到绿灯 C、抛掷一枚硬币,出现正面朝上 D、若今天是星期一,则明天是星期二2. 下列方程一定是一元二次方程的是( )A、x2﹣1=0 B、x+y=1 C、 D、3. 将抛物线y=x2的图像向下平移2个单位长度,得到的抛物线的解析式为( )A、y=(x-2)2 B、y=(x+2)2 C、y=x2+2 D、y=x2﹣24. 如图,⊙O中,弦AB、CD相交于点P,∠A=35°,则∠D的大小是( )
 A、15° B、20° C、35° D、40°5. 对于二次函数y=3(x﹣1)2的图象,下列说法正确的是( )A、开口向下 B、图像关于直线当x=1对称 C、当x=1时,y的值最大 D、顶点坐标是(0,1)6. 如图:点D是△ABC边BC上一点,下列条件中,能使△ABC∽△DAC的是( )
A、15° B、20° C、35° D、40°5. 对于二次函数y=3(x﹣1)2的图象,下列说法正确的是( )A、开口向下 B、图像关于直线当x=1对称 C、当x=1时,y的值最大 D、顶点坐标是(0,1)6. 如图:点D是△ABC边BC上一点,下列条件中,能使△ABC∽△DAC的是( ) A、∠1=∠C B、∠BAC=∠BDA; C、AC2=CD•CB. D、AD2=BD•CD;7. 如图,PA、PB是⊙O的两条切线,切点分别是A、B,且∠APB=60°,⊙O的半径为3,则阴影部分的面积为( )
A、∠1=∠C B、∠BAC=∠BDA; C、AC2=CD•CB. D、AD2=BD•CD;7. 如图,PA、PB是⊙O的两条切线,切点分别是A、B,且∠APB=60°,⊙O的半径为3,则阴影部分的面积为( )
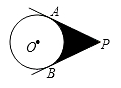 A、 B、 C、18-6π D、18-3π8. 在平面直角坐标系中,已知点A(-4,2),B(-2,-1),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )A、(2,-1) B、(8,-4) C、(2,-1)或(-2,1) D、(8,-4)或(-8,4)9. 计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
A、 B、 C、18-6π D、18-3π8. 在平面直角坐标系中,已知点A(-4,2),B(-2,-1),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )A、(2,-1) B、(8,-4) C、(2,-1)或(-2,1) D、(8,-4)或(-8,4)9. 计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图: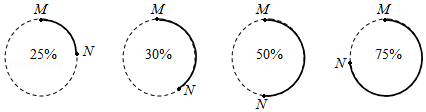
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A、d(25%)=1 B、当x>50%时,d(x)>1 C、当x1>x2时,d(x1)>d(x2) D、当x1+x2=100%时,d(x1)=d(x2)10. 如图1,在正方形ABCD中,点F为对角线BD上一点,EF⊥AB于点E,将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,则在图2中,以下说法:①FD= AE;②∠AEB=135°;③S△AEB:S△DFB=1:2;④AE∥BF,正确结论的序号( ) A、①② B、①③ C、②③ D、③④
A、①② B、①③ C、②③ D、③④二、填空题(共4小题)
-
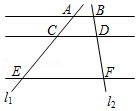
11. 点(2,-3)关于原点对称的点的坐标为12. 某个密码锁的密码由三个数字组成,每个数字都是0﹣9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开.如果仅忘记了锁设密码的最后那个数字,那么一次就能打开该密码的概率是13. 如图,AB∥CD∥EF,直线AE、BF被这组平行线所截,.已知AC=4, 则CE的长为.
 14. 有一种流感病毒,刚开始有2人患了流感,经过两轮传染后共有128人患流感.如果设每轮传染中平均一个人传染x个人,那么可列方程为.15. 如图,等边△ABC的边长为a的正三角形A1B1C1绕它的中心旋转,旋转后得到△A2B2C2则两个三角形的重叠部分面积的最小值为
14. 有一种流感病毒,刚开始有2人患了流感,经过两轮传染后共有128人患流感.如果设每轮传染中平均一个人传染x个人,那么可列方程为.15. 如图,等边△ABC的边长为a的正三角形A1B1C1绕它的中心旋转,旋转后得到△A2B2C2则两个三角形的重叠部分面积的最小值为 16. 我们把二次函数y=ax2+bx+c的各项系数的平方和叫做魅力值,记作M=a2+b2+c2 , 已知二次函数y=ax2+bx+c(a>0)的图像经过点A(1,2)与点B(2,c+10),且与x轴有两个不同的交点,则M的取值范围
16. 我们把二次函数y=ax2+bx+c的各项系数的平方和叫做魅力值,记作M=a2+b2+c2 , 已知二次函数y=ax2+bx+c(a>0)的图像经过点A(1,2)与点B(2,c+10),且与x轴有两个不同的交点,则M的取值范围三、解答题(共8小题)
-
17. 解方程:(1)、2x2-8=0(2)、x2-3x+1=018. 如图,在正方形网格中,按要求完成以下图,
 (1)、在图1中,线段AB的两个端点与点O均在格点上,作线段AB关于点O对称的线段A’B’:(2)、在图2中,△ABC的顶点均在格点上,作△ABC绕点A旋转一定角度后,顶点仍都在格点上的△AB’C’19. 如图,△ABC中,DE∥BC,EF∥AB
(1)、在图1中,线段AB的两个端点与点O均在格点上,作线段AB关于点O对称的线段A’B’:(2)、在图2中,△ABC的顶点均在格点上,作△ABC绕点A旋转一定角度后,顶点仍都在格点上的△AB’C’19. 如图,△ABC中,DE∥BC,EF∥AB
求证:△ADE∽△EFC.
20. 已知关于x的方程x2-mx+m﹣3=0.(1)、若该方程的一个根为-2,求m的值(2)、求证:不论m取何实数,该方程都有两个不相等的实数根.21. 甲、乙、丙、丁四个人玩传球游戏,球从一人手上随机传到另外一个人手中记作传球一次,开始时球在甲手中.(1)、经过一次传球后,球落在乙的手中的概率是多少?(2)、若请用画树状图或列表等方法求“经过两次传球后,球回到甲手中”的概率.22. 如图,以△ABC的边BC上一点O为圆心的⊙O经过A,B两点,且与BC边交于点E,OD垂直于BE交⊙O于点D,弦AD交BC与点F,AC=FC. (1)、求证:AC是⊙O的切线;(2)、已知圆的半径为3,EF=2,点G是弦AD的中点,求OG的长.23. 网络销售已经成为一种比较热门的销售方式,某电商购进一种单价30元的商品,为减少库存.未来30天,这种商品将开展“每天降价1元”的促销活动,即从活动开始的第一天起每天的销售单价均比前一天降1元,通过市场调查发现,该商品的销售单价每降1元,每天销售量增加3件,活动前的销售单价为100元,每天销售15件,设活动开始后的第t天(t为正整数)所获的利润为w(元).(1)、求出w与t之间的函数关系式;(2)、哪一天所获利润最大,最大利润是多少元?(3)、若每销售一件商品需缴纳电商平台推广费用a元(a>0),在这30天内,要使每天缴纳电商平台推广费用后的利润随着t的增大而则增大,求a的取值范围.24. 如图1,点M是正方形ABCD的对角线AC上的一点,射线DM与△AMB的外接圆的另一个交点为N,与射线CB相交于点p.
(1)、求证:AC是⊙O的切线;(2)、已知圆的半径为3,EF=2,点G是弦AD的中点,求OG的长.23. 网络销售已经成为一种比较热门的销售方式,某电商购进一种单价30元的商品,为减少库存.未来30天,这种商品将开展“每天降价1元”的促销活动,即从活动开始的第一天起每天的销售单价均比前一天降1元,通过市场调查发现,该商品的销售单价每降1元,每天销售量增加3件,活动前的销售单价为100元,每天销售15件,设活动开始后的第t天(t为正整数)所获的利润为w(元).(1)、求出w与t之间的函数关系式;(2)、哪一天所获利润最大,最大利润是多少元?(3)、若每销售一件商品需缴纳电商平台推广费用a元(a>0),在这30天内,要使每天缴纳电商平台推广费用后的利润随着t的增大而则增大,求a的取值范围.24. 如图1,点M是正方形ABCD的对角线AC上的一点,射线DM与△AMB的外接圆的另一个交点为N,与射线CB相交于点p.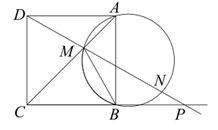
 (1)、当点N与点B重合时,则 的值为(2)、当MN是△AMB外接圆的直径时,求 的值;(3)、设 =k, =y,求y与k的函数解析式(4)、当点M从C运动到A时,点M的运动路线长记为m,点N的运动路线记作n,请直接写出 的值.
(1)、当点N与点B重合时,则 的值为(2)、当MN是△AMB外接圆的直径时,求 的值;(3)、设 =k, =y,求y与k的函数解析式(4)、当点M从C运动到A时,点M的运动路线长记为m,点N的运动路线记作n,请直接写出 的值.