广东省深圳市福田区十二校联考2019-2020学年九年级下学期数学6月月考试卷
试卷更新日期:2021-02-20 类型:月考试卷
一、单选题
-
1. 下列四个数:﹣2,﹣0.6, , 中,绝对值最小的是( )A、﹣2 B、﹣0.6 C、 D、2. 在国家大数据战略的引领下,我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储58000000000本书籍,将58000000000用科学记数法表示应为( )A、 B、 C、 D、3. 若实数a , b , c , d在数轴上的对应点的位置如图所示,则正确的结论是( )
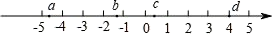 A、 B、 C、 D、4. 如果一个正多边形的内角和等于 ,那么该正多边形的一个外角等于( )A、 B、 C、 D、5. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、 B、 C、 D、4. 如果一个正多边形的内角和等于 ,那么该正多边形的一个外角等于( )A、 B、 C、 D、5. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )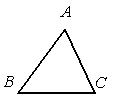 A、
A、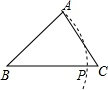 B、
B、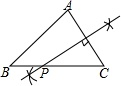 C、
C、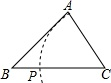 D、
D、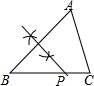 6. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
6. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )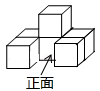 A、
A、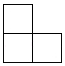 B、
B、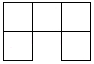 C、
C、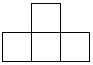 D、
D、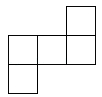 7. 如图为某队员射击10次的成绩统计图,该队员射击成绩的众数与中位数分别是( )
7. 如图为某队员射击10次的成绩统计图,该队员射击成绩的众数与中位数分别是( ) A、8,7.5 B、8,7 C、7,7.5 D、7,78. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、
A、8,7.5 B、8,7 C、7,7.5 D、7,78. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、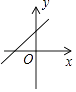 B、
B、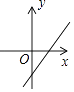 C、
C、 D、
D、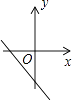 9. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点 ,则 和 的面积之差 为( )
9. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点 ,则 和 的面积之差 为( ) A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最小值是( )
A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最小值是( )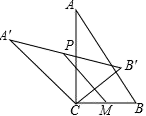 A、1 B、2 C、3 D、411. 如图,线段AB是直线y=x+1的一部分,其中点A在y轴上,点B横坐标为2,曲线BC是双曲线 ( )的一部分,由点C开始不断重复“A−B−C”的过程,形成一组波浪线,点P(2019,m)与Q(2025,n)均在该波浪线上,G为x轴上一动点,则△PQG周长的最小值为( )
A、1 B、2 C、3 D、411. 如图,线段AB是直线y=x+1的一部分,其中点A在y轴上,点B横坐标为2,曲线BC是双曲线 ( )的一部分,由点C开始不断重复“A−B−C”的过程,形成一组波浪线,点P(2019,m)与Q(2025,n)均在该波浪线上,G为x轴上一动点,则△PQG周长的最小值为( )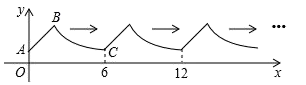 A、16 B、 C、 D、12. 如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF= ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
A、16 B、 C、 D、12. 如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF= ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )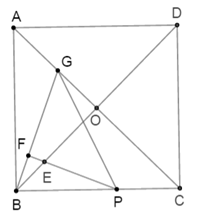
① ;②PE=2BF;③在点P运动的过程中,当GB=GP时, ;④当P为BC的中点时, .
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
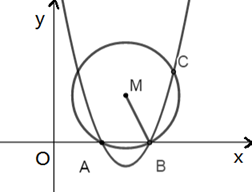
13. 若x2+x﹣3=0,则代数式2(x﹣2)(x+2)﹣x(x﹣1)的值是 .14. 从n个苹果和4个雪梨中,任选1个,若选中苹果的概率是 ,则n的值是.15. 如图所示,抛物线 与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为.
 16. 如图,矩形ABCD中,BC=4,且AB= ,连接对角线AC,点E为AC中点,点F为线段AB上的动点,连接EF,作点C关于EF的对称点C',连接C'E,C'F,若△EFC'与△ACF的重叠部分(△EFG)面积等于△ACF的 ,则BF= .
16. 如图,矩形ABCD中,BC=4,且AB= ,连接对角线AC,点E为AC中点,点F为线段AB上的动点,连接EF,作点C关于EF的对称点C',连接C'E,C'F,若△EFC'与△ACF的重叠部分(△EFG)面积等于△ACF的 ,则BF= .
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 .19. 学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).
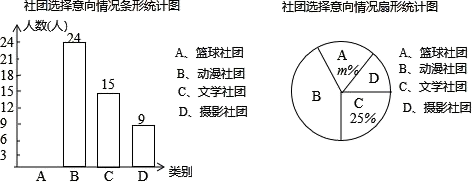
请根据图中信息,解答下列问题:
(1)、求扇形统计图中m的值,并补全条形统计图;(2)、在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为.(3)、已知该校有1200名学生,请估计“文学社团”共有多少人?20. 如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.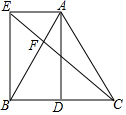 (1)、求证:四边形AEBD是矩形;(2)、连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.21. 为了迎接“五•一”小长假的购物高峰.某服装专卖店老板小王准备购进甲、乙两种夏季服装.其中甲种服装每件的成本价比乙种服装的成本价多20元,甲种服装每件的售价为240元比乙种服装的售价多80元.小王用4000元购进甲种服装的数量与用3200元购进乙种服装的数量相同.(1)、甲种服装每件的成本是多少元?(2)、要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21100元,且不超过21700元,问小王有几种进货方案?22. 如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.
(1)、求证:四边形AEBD是矩形;(2)、连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.21. 为了迎接“五•一”小长假的购物高峰.某服装专卖店老板小王准备购进甲、乙两种夏季服装.其中甲种服装每件的成本价比乙种服装的成本价多20元,甲种服装每件的售价为240元比乙种服装的售价多80元.小王用4000元购进甲种服装的数量与用3200元购进乙种服装的数量相同.(1)、甲种服装每件的成本是多少元?(2)、要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21100元,且不超过21700元,问小王有几种进货方案?22. 如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.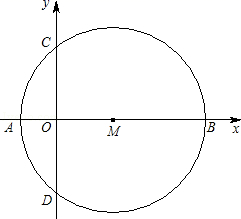 (1)、若C点坐标为(0,4),求点A坐标.(2)、在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.(3)、过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.23. 抛物线y=﹣ x2﹣ x+ 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)、若C点坐标为(0,4),求点A坐标.(2)、在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.(3)、过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.23. 抛物线y=﹣ x2﹣ x+ 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.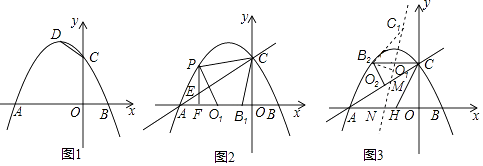 (1)、如图1,连接CD,求线段CD的长;
(1)、如图1,连接CD,求线段CD的长;
(2)、如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1 , 当PE+ EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)、如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2 , C的对应点分别是点O3 , C1 , 直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.