广东省华南师大中山附中2019-2020学年九年级下学期数学3月月考试卷
试卷更新日期:2021-02-20 类型:月考试卷
一、单选题
-
1. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 去年汕头市经济发展成绩斐然,全市投资总额首次突破200 000 000 000元,其中200 000 000 000用科学记数法表示为( )A、2×1012 B、0.2×1012 C、2×1011 D、20×10113. 下列计算正确的是( )A、 B、 C、 D、4. 下列根式中与 是同类二次根式的是( )A、 B、 C、 D、5. 在△ABC中,∠C=90°,BC=2,sinA= ,则边AC的长是( )A、 B、3 C、 D、6. 已知点A(5,-2)关于y轴的对称点A′在反比例函数y= (k≠0)的图象上,则实数k的值为( )A、10 B、﹣10 C、 D、﹣7. 如图所示,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若∠DEF=55°,则∠A的度数是( ).
2. 去年汕头市经济发展成绩斐然,全市投资总额首次突破200 000 000 000元,其中200 000 000 000用科学记数法表示为( )A、2×1012 B、0.2×1012 C、2×1011 D、20×10113. 下列计算正确的是( )A、 B、 C、 D、4. 下列根式中与 是同类二次根式的是( )A、 B、 C、 D、5. 在△ABC中,∠C=90°,BC=2,sinA= ,则边AC的长是( )A、 B、3 C、 D、6. 已知点A(5,-2)关于y轴的对称点A′在反比例函数y= (k≠0)的图象上,则实数k的值为( )A、10 B、﹣10 C、 D、﹣7. 如图所示,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若∠DEF=55°,则∠A的度数是( ). A、35° B、55° C、70° D、125°8. 如图1是由大小相同的小正方体搭成的几何体,将它左侧的小正方体移动后得到图2.关于移动前后的几何体的三视图,下列说法正确的是( )
A、35° B、55° C、70° D、125°8. 如图1是由大小相同的小正方体搭成的几何体,将它左侧的小正方体移动后得到图2.关于移动前后的几何体的三视图,下列说法正确的是( ) A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同9. 如图,△ABC,△FGH中,D,E两点分别在AB,AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )
A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图都不相同9. 如图,△ABC,△FGH中,D,E两点分别在AB,AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )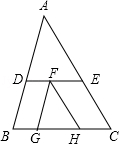 A、2:1 B、3:2 C、5:2 D、9:410. 如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A、2:1 B、3:2 C、5:2 D、9:410. 如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( ) A、3 B、2 C、 D、1
A、3 B、2 C、 D、1二、填空题
-
11. 比较大小:2 5(填“>,<,=”).12. 若 ,则代数式 的值为.13. 分解因式:4a2-4a+1= .14. 已知tan(α+15°)= ,则tanα的值为 .15. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
 16. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线分别交边BC,AB于点D,E.如果BC=18,tanA= ,那么CD= .
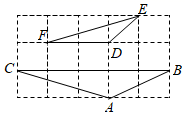
16. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线分别交边BC,AB于点D,E.如果BC=18,tanA= ,那么CD= . 17. 如图,若 内一点 满足 ,则称点P为 的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知 中, , , 为 的布罗卡尔点,若 ,则 .
17. 如图,若 内一点 满足 ,则称点P为 的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知 中, , , 为 的布罗卡尔点,若 ,则 .
三、解答题
-
18. 计算: +(﹣ )﹣3tan30°﹣(π﹣ )0 .19. 先化简,再求值:(1﹣ )÷ ,其中a= ﹣1.20. 在△ABC中,AB=8,BC=6,∠B为锐角且cosB= .
 (1)、求△ABC的面积.(2)、求tanC.21. 如图所示,小红想利用竹竿来测量旗杆AB的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为4 米,∠DCE=45°,求旗杆AB的高度?
(1)、求△ABC的面积.(2)、求tanC.21. 如图所示,小红想利用竹竿来测量旗杆AB的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为4 米,∠DCE=45°,求旗杆AB的高度?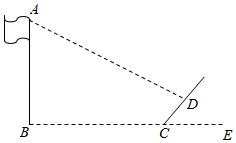 22. 如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
22. 如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F. (1)、求证:△ECD∽△DEF;(2)、若CD=4,求AF的长.23. 已知:如图所示,一次函数y=﹣2x的图象与反比例函数y= 的图象分别交于点A和点B,过点B作BC⊥y轴于点C,点E是x轴的正半轴上的一点,且S△BCE=2,∠AEB=90°.
(1)、求证:△ECD∽△DEF;(2)、若CD=4,求AF的长.23. 已知:如图所示,一次函数y=﹣2x的图象与反比例函数y= 的图象分别交于点A和点B,过点B作BC⊥y轴于点C,点E是x轴的正半轴上的一点,且S△BCE=2,∠AEB=90°. (1)、求m的值及点E的坐标;(2)、连接AC,求△ACE的面积.24. 如图,在⊙O中,直线CD垂直直径AB于E,直线GF为⊙O的切线,切点为H,GF与直线CD相交于点F,与AB延长线交于点G,AH交CD于M,其中MH2=MD·MF.
(1)、求m的值及点E的坐标;(2)、连接AC,求△ACE的面积.24. 如图,在⊙O中,直线CD垂直直径AB于E,直线GF为⊙O的切线,切点为H,GF与直线CD相交于点F,与AB延长线交于点G,AH交CD于M,其中MH2=MD·MF. (1)、连接OH,求证:△FMH为等腰三角形;(2)、求证:AC//FG;(3)、若cosF= ,AM=2 ,求线段GH的长.25. 在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+(k﹣1)x+k(k>0)交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的正半轴于点C,且AB=4.
(1)、连接OH,求证:△FMH为等腰三角形;(2)、求证:AC//FG;(3)、若cosF= ,AM=2 ,求线段GH的长.25. 在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+(k﹣1)x+k(k>0)交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的正半轴于点C,且AB=4. (1)、如图1,求k的值;(2)、如图2,点D在第一象限的抛物线上,点E在线段BC上,DE//y轴,若DE= BE,求点D的坐标;(3)、如图3,在(2)的条件下,F为抛物线顶点,点P在第四象限的抛物线上,FP交直线DE于点Q,点G与点D关于y轴对称,若GQ=DP,求点P的坐标.
(1)、如图1,求k的值;(2)、如图2,点D在第一象限的抛物线上,点E在线段BC上,DE//y轴,若DE= BE,求点D的坐标;(3)、如图3,在(2)的条件下,F为抛物线顶点,点P在第四象限的抛物线上,FP交直线DE于点Q,点G与点D关于y轴对称,若GQ=DP,求点P的坐标.