广东省高州市七校2019-2020学年九年级下学期数学5月月考试卷
试卷更新日期:2021-02-20 类型:月考试卷
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、±3 D、2. 举世瞩目的港珠澳大桥于2018年10月24日正式开通营运,它是迄今为止世界上最长的跨海大桥,全长约55000米.55000这个数用科学记数法可表示为( )A、5.5×103 B、55×103 C、0.55×105 D、5.5×1043. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 数据2、3、4、7、7的中位数与众数分别是( )A、2,3 B、3,4 C、4,7 D、2,75. 下列计算正确的是( )A、 B、 C、 D、6. 如图,平行线 , 被直线 所截, ,则 的度数是( )
4. 数据2、3、4、7、7的中位数与众数分别是( )A、2,3 B、3,4 C、4,7 D、2,75. 下列计算正确的是( )A、 B、 C、 D、6. 如图,平行线 , 被直线 所截, ,则 的度数是( )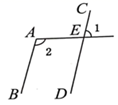 A、 B、 C、 D、7. 如图, 中, , , ,则 的长度为( )
A、 B、 C、 D、7. 如图, 中, , , ,则 的长度为( )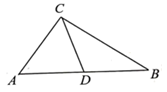 A、 B、 C、 D、8. 二次函数y=3(x﹣h)2+k的图象如图所示,下列判断正确的是( )
A、 B、 C、 D、8. 二次函数y=3(x﹣h)2+k的图象如图所示,下列判断正确的是( )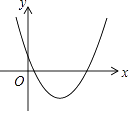 A、h>0,k>0 B、h>0,k<0 C、h<0,k>0 D、h<0,k<09. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、10. 如图,在菱形 中, , , 分别交 、 于点 、 , ,连结 ,以下结论:① ;②点 到 的距离是 ;③ 与 的面积比为 ;④ 的面积为 ,其中一定成立的个数为( )
A、h>0,k>0 B、h>0,k<0 C、h<0,k>0 D、h<0,k<09. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、10. 如图,在菱形 中, , , 分别交 、 于点 、 , ,连结 ,以下结论:① ;②点 到 的距离是 ;③ 与 的面积比为 ;④ 的面积为 ,其中一定成立的个数为( )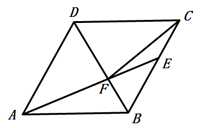 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
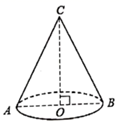
11. 分解因式: .12. 在函数y= 中,自变量x的取值范围是 .13. 已知 ,则整式 的值为 .14. 不等式组 的解集是 .15. 如图,用纸板做一个圆锥形漏斗模型,它的底面半径 ,高 ,则这个圆锥漏斗的侧面积为(结果保留 )
 16. 如图, 中, , , ,现将 沿 折叠,使点 与点 重合,则 的值是 .
16. 如图, 中, , , ,现将 沿 折叠,使点 与点 重合,则 的值是 . 17. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有 个小圆圈,第②个图形中一共有 个小圆圈,第③个图形中一共有 个小圆圈,……,按此规律排列,则第⑨个图形中小圆圈的个数为 .
17. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有 个小圆圈,第②个图形中一共有 个小圆圈,第③个图形中一共有 个小圆圈,……,按此规律排列,则第⑨个图形中小圆圈的个数为 .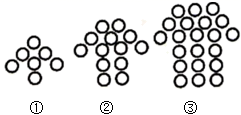
三、解答题
-
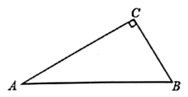
18. 计算:19. 先化简,再求值: ,其中x= +1.20. 如图,在 中, .
 (1)、用尺规作图法作 的平分线 ,交 于点 ;(保留作图痕迹,不要求写作法和证明)(2)、若 ,求 .21. 某初中为了提高学生综合素质,决定开设以下校本课程: .软笔书法, .经典诵读, .钢笔画, .花样跳绳,为了了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行了调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)、用尺规作图法作 的平分线 ,交 于点 ;(保留作图痕迹,不要求写作法和证明)(2)、若 ,求 .21. 某初中为了提高学生综合素质,决定开设以下校本课程: .软笔书法, .经典诵读, .钢笔画, .花样跳绳,为了了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行了调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: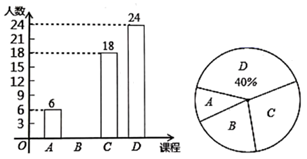 (1)、这次被调查的学生共人;(2)、请将条形统计补充完整;(3)、在平时的花样跳绳的课堂学习中,甲、乙、丙三人表现优秀,现决定从这三名同学中任选两名参加全区综合素质展示,求恰好同时选中甲、乙两位同学的概率.22. 某小区为更好地提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需540元,且每个温馨提示牌比垃圾箱便宜 元.(1)、问购买 个温馨提示牌和 个垃圾箱各需多少元?(2)、如果需要购买温馨提示牌和垃圾箱共 个费用不超过 元,求最多购买垃圾箱多少个.23. 如图,一次函数 与反比例函数 的图象交于点 和 .
(1)、这次被调查的学生共人;(2)、请将条形统计补充完整;(3)、在平时的花样跳绳的课堂学习中,甲、乙、丙三人表现优秀,现决定从这三名同学中任选两名参加全区综合素质展示,求恰好同时选中甲、乙两位同学的概率.22. 某小区为更好地提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需540元,且每个温馨提示牌比垃圾箱便宜 元.(1)、问购买 个温馨提示牌和 个垃圾箱各需多少元?(2)、如果需要购买温馨提示牌和垃圾箱共 个费用不超过 元,求最多购买垃圾箱多少个.23. 如图,一次函数 与反比例函数 的图象交于点 和 .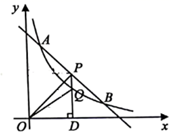 (1)、求反比例函数和一次函数的解析式;(2)、点 是线段 上一点,过点 作 轴于点 ,交反比例函数图象于点 ,连接 、 ,若 的面积为 ,求 点的坐标.24. 如图,在 中, , 平分 交 于点 ,点 为 上一点,经过点 , 的 分别交 , 于点 , ,连接 ,连接 交 于点 .
(1)、求反比例函数和一次函数的解析式;(2)、点 是线段 上一点,过点 作 轴于点 ,交反比例函数图象于点 ,连接 、 ,若 的面积为 ,求 点的坐标.24. 如图,在 中, , 平分 交 于点 ,点 为 上一点,经过点 , 的 分别交 , 于点 , ,连接 ,连接 交 于点 .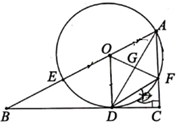 (1)、求证: 是 的切线;(2)、设 , ,试用含 , 的代数式表示线段 的长;(3)、若 , ,求 的长.25. 如图,在矩形 中, , .如果点 由点 出发沿 方向向点 匀速运动,同时点 由点 出发沿 方向向点 匀速运动,它们的速度分别为 和 .过点 作 ,分别交 、 于点 和 ,设运动时间为 .
(1)、求证: 是 的切线;(2)、设 , ,试用含 , 的代数式表示线段 的长;(3)、若 , ,求 的长.25. 如图,在矩形 中, , .如果点 由点 出发沿 方向向点 匀速运动,同时点 由点 出发沿 方向向点 匀速运动,它们的速度分别为 和 .过点 作 ,分别交 、 于点 和 ,设运动时间为 . (1)、连结 、 ,若四边形 为平行四边形,求 的值;(2)、连结 ,设 的面积为 ,求 与 的函数关系式,并求 的最大值;(3)、若 与 相似,求出 的值.
(1)、连结 、 ,若四边形 为平行四边形,求 的值;(2)、连结 ,设 的面积为 ,求 与 的函数关系式,并求 的最大值;(3)、若 与 相似,求出 的值.