广东省华南师大中山附中2019-2020学年八年级下学期数学第二次月考试卷

试卷更新日期：2021-02-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列计算正确的是（　　）

A、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$ B、2 $\sqrt{2} - \sqrt{2} = 2$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = \sqrt{6}$

查看试题解析
2. 下列根式中属于最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\sqrt{27 x}$

查看试题解析
3. 下列各组数中，能构成直角三角形的是（）

A、4，5，6 B、1，1， $\sqrt{2}$ C、6，8，11 D、5，12，23

查看试题解析
4. 如图所示，数轴上点 $A$ 所表示的数为 $a$ ，则 $a$ 的值是（）

A、 $\sqrt{5} + 1$ B、 $- \sqrt{5} + 1$ C、 $\sqrt{5} - 1$ D、 $\sqrt{5}$

查看试题解析
5. 如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOD=120°，AC=4，则CD的长为（）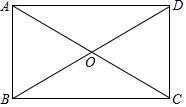

A、2 B、3 C、2 $\sqrt{2}$ D、2 $\sqrt{3}$

查看试题解析
6. 如图，在平行四边形ABCD中，AB＝6cm，AD＝8cm，AC、BD相交于点O，OE⊥BD交AD于E，则△ABE的周长为（）．

A、12cm B、14cm C、16cm D、28cm

查看试题解析
7. 如图，在四边形ABCD中，点O是对角线的交点，能判定这个四边形是正方形的是（）

A、AC=BD，AB∥CB，AD∥BC B、AD∥BC，∠BAD =∠BCD C、AO=CO，BO=DO，AB=BC D、AO=BO=CO=DO，AC⊥BD

查看试题解析
8. 下列各命题中，原命题成立，而它逆命题不成立的是（）

A、平行四边形的两组对边分别平行 B、矩形的对角线相等 C、四边相等的四边形是菱形 D、直角三角形中，斜边的平方等于两直角边的平方和

查看试题解析
9. 如图，在正方形ABCD中，E是AB上一点，BE＝2，AE＝4，P是AC上一动点，则PB+PE的最小值是（）

A、6 B、2 $\sqrt{5}$ C、8 D、2 $\sqrt{13}$

查看试题解析
10. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，AD＝ $\frac{1}{2}$ AC，M、N、P分别是OA、OB、CD的中点，下列结论：
①CN⊥BD；

②MN＝NP；

③四边形MNCP是菱形；

④ND平分∠PNM．

其中正确的有（）

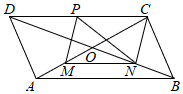A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

11. 化简 $\sqrt{{(2 - \sqrt{5})}^{2}}$ =

查看试题解析
12. 若二次根式 $\sqrt{3 - 4 x}$ 有意义，则x的取值范围是．

查看试题解析
13. 如图，四边形ABCD的两条对角线AC、BD互相垂直，A₁、B₁、C₁、D₁是四边形ABCD的中点．如果AC＝ $\sqrt{6}$ ，BD＝4 $\sqrt{3}$ ，那么四边形A₁B₁C₁D₁的面积为．

查看试题解析
14. 《九章算术》是我国古代最重要的数学著作之一，在“勾股”章节中记载了一道“折竹抵地”的问题：“今有竹高一尺，末折抵地，去本三尺，问折者高几何？”译文：一根竹子，原高一丈，后来竹子折断，其竹竿恰好着地，着地处离原竹子根部3尺远，如图所示，问：原处竹子（ $A C$ ）还剩尺？（1丈=10尺）．

查看试题解析
15. 如图，正方形ABCO的顶点C，A分别在轴，轴上，BC是菱形BDCE的对角线，若∠D=60°，BC=2，则点D的坐标是．

查看试题解析
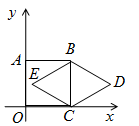16. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝7，BC＝10，则EF的长为.

查看试题解析
17. 在菱形ABCD中，∠BAD＝108°，AB的垂直平分线交AC于点N，点M为垂足，连接DN，则∠CDN的度数是．

查看试题解析

三、解答题

18. 计算：

(1)、 $(\sqrt{24} - 5 \sqrt{\frac{1}{5}}) - (4 \sqrt{1 \frac{1}{2}} - \sqrt{45})$ ；

(2)、 $4 \sqrt{\frac{2}{3}} \times \sqrt{75} - (\sqrt{48} + \sqrt{6}) \div \sqrt{3}$ ．

查看试题解析
19. 如图，在△ABC中，CD⊥AB，垂足为D，如果CD＝6，AD＝9，BD＝4，那么△ABC是直角三角形吗？请说明理由．

查看试题解析
20. 如图，在▱ABCD中，O是BD的中点，E、F分别是BC、AD的中点，M、N分别是OB、OD中点．求证：四边形MENF是平行四边形．

查看试题解析
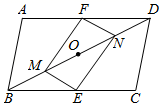21. 如图，菱形ABCD的对角线AC与BD相交于O，E是BC中点，连接OE并延长到F，使EF＝OE．

(1)、求证：四边形OBFC是矩形．

(2)、如果作BG∥OF，FG∥BC，四边形BGFE是何特殊四边形？并说明理由．

查看试题解析
22. 一张矩形纸ABCD，将点B翻折到对角线AC上的点M处，折痕CE交AB于点E．将点D翻折到对角线AC上的点H处，折痕AF交DC于点F，折叠出四边形AECF．

(1)、求证：AF $//$ CE；

(2)、当∠BAC等于多少度时，四边形AECF是菱形？说明理由．

查看试题解析
23. 如图，已知正方形ABCD的面积是8，连接AC、BD交于点O，CM平分∠ACD交BD于点M，MN⊥CM，交AB于点N，

(1)、求∠BMN的度数；

(2)、求BN的长．

查看试题解析
24. 已知△ABC的三边BC＝a，AC＝b，AB＝c，且满足|a- $\sqrt{13}$ |+ $\sqrt{b - 2}$ +（c-3）²＝0．如图，P为BC边上一动点，PM⊥AB于点M，PN⊥AC于点N．

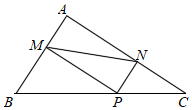(1)、求证：四边形AMPN是矩形；

(2)、在点P的运动过程中，MN的长度是否存在最小值？若存在，请求出最小值，若不存在，请说明理由．

查看试题解析
25. 如图1，在平行四边形ABCD中，∠ADC的平分线交AB于点E，交CB的延长线于F，以BE、BF为邻边作▱EBFH．

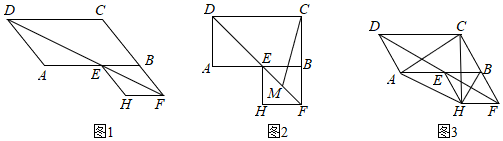(1)、证明：▱EBFH是菱形；

(2)、（如图2）若∠ABC＝90°．
①直接写出四边形EBHF的形状；

②已知AB＝10，AD＝6，M是EF的中点，求CM的长．

(3)、（如图3）若∠ABC＝60°，连结HA、HB、HC、AC，求证：△ACH是等边三角形．

查看试题解析