广东省佛山市南海区2019-2020学年八年级下学期数学月考试卷

试卷更新日期：2021-02-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 若 $a > b ，$ 下列说法正确的是（）

A、 $a + 1 < b + 1$ B、 $2 a < 2 b$ C、 $- 2 a < - 2 b$ D、 $a - 1 < b - 1$

查看试题解析
2. 在数轴上表示不等式﹣2≤x＜4，正确的是（）

A、 B、 C、 D、

查看试题解析
3. 下列等式，从左到右的变形，属于因式分解的是（）

A、 $6 x^{2} y^{3} = 2 x^{2} \cdot 3 y^{3}$ B、 $a (a + 1) (a - 1) = a^{3} - a$ C、 $a^{2} - 2 a + 1 = {(a - 1)}^{2}$ D、 $x^{2} + 1 = x (x + \frac{1}{x})$

查看试题解析
4. 如图， $∠ A = 36^{\circ}$ ， $∠ D B C = 36^{\circ}$ ， $∠ C = 72^{\circ}$ ，则图中等腰三角形有（）

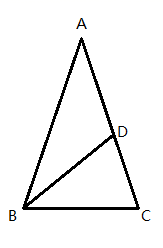A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 不能判定四边形 $A B C D$ 为平行四边形的条件是（）

A、 $A B / / C D ， A D / / B C$ B、 $A B = C D ， A D = B C$ C、 $A D / / B C ， A D = B C$ D、 $A B / / C D ， A D = B C$

查看试题解析
6. 在平面直角坐标系中，把点 $P (- 5 ， 2)$ 先向左平移3个单位长度，再向上平移2个单位长度后得到的点的坐标是（）

A、 $(- 8 ， 4)$ B、 $(- 8 ， 0)$ C、 $(- 2 ， 4)$ D、 $(- 2 ， 0)$

查看试题解析
7. 如图，是某商场一楼与二楼之间的手扶电梯示意图.其中 $A B 、 C D$ 分别表示一楼、二楼地面的水平线， $∠ A B C = 150 ° ， B C$ 的长是 $40 m ，$ 则乘电梯从点 $B$ 到点 $C$ 上升的高度h是（）m

A、 $20$ B、 $40$ C、 $80$ D、 $20 \sqrt{3}$

查看试题解析
8. 若分式 $\frac{3}{x + 2}$ 有意义，则 $x$ 应满足的条件是（）

A、 $x \neq 0$ B、 $x \neq - 2$ C、 $x \geq - 2$ D、 $x \leq - 2$

查看试题解析
9. 如图，边长为 $a ， b$ 的矩形的周长为 $14$ ，面积为10，则 $a^{2} b + a b^{2}$ 的值为（）

A、36 B、 $70$ C、 $35$ D、 $24$

查看试题解析
10. 牛顿曾说过：“反证法是数学家最精良的武器之一．”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于60°”时，第一步先假设（）

A、三角形中有一个内角小于60° B、三角形中有一个内角大于60° C、三角形中每个内角都大于60° D、三角形中没有一个内角小于60°

查看试题解析

二、填空题

11. 分解因式： $2 a - a b =$ ．

查看试题解析
12. 如果代数式 $\frac{| m | - 1}{m + 1}$ 的值为0，则m的值为．

查看试题解析
13. 等腰三角形的一边长7cm，另一边长8cm，那么这个三角形的周长是cm．

查看试题解析
14. 如图，将 $Δ A B C$ 绕点 $A$ 顺时针旋转 $60^{\circ}$ 得到 $Δ A E D$ ，则 $∠ C A D =$ $^{\circ}$

查看试题解析
15. 如图，将 $▱ ABCO$ 放置在平面直角坐标系 $xOy$ 中，O为坐标原点，若点 $A$ 的坐标是（5，0）．点 $C$ 的坐标为（1，－3），则点 $B$ 的坐标是；

查看试题解析
16. 一次函数 $y_{1} = a x + 3$ 与 $y_{2} = k x - 1$ 的图象如图所示，则不等式 $a x + 3 > k x - 1$ 的解集是．

查看试题解析
17. 如图已知： $∠ M O N = 30 ° ，$ 点 $A_{1} ， A_{2} ， A_{3} ，$ ···，在射线 $O N$ 上，点 $B_{1} 、 B_{2} 、 B_{3}$ ，···，在射线 $O M$ 上， $△ A_{1} B_{1} B_{2} ， △ A_{2} B_{2} B_{3} ， △ A_{3} B_{3} B_{4}$ ，···，均为等边三角形，若 $O B_{1} = 1 ，$ 则 $△ A_{8} B_{8} B_{9} ，$ 的边长为．

查看试题解析

三、解答题

18. 解不等式组： ${\begin{array}{l} 3 x > 4 (x - 1) \\ \frac{x + 1}{2} ⩽ x \end{array}$ ．

查看试题解析
19. 因式分解： $x (x - 4) + 4$

查看试题解析
20. 平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (1 ， 1) 、 B (5 ， 1) 、 C (4 ， 4)$ .

按下列要求画图：

①将 $△ A B C$ 向下平移 $5$ 个单位得到 $△ A_{1} B_{1} C_{1} ，$ 并写出点 $A_{1}$ 的坐标；

②将 $△ A B C$ 绕原点 $O$ 逆时针旋转 $90 °$ 后得到 $△ A_{2} B_{2} C_{2} ，$ 并写出点 $B_{2}$ 的坐标；

查看试题解析
21. 先化简： $(\frac{3 x}{x - 2} - \frac{x}{x + 2}) \cdot \frac{x^{2} - 4}{x}$ ，并在 $- 2 ， 0 ， 1 ， 2$ 中选一个合适的数求值.

查看试题解析
22. 如图，在 $Δ A B C$ 和 $Δ D C B$ 中， $∠ A = ∠ D = 90^{°}$ ， $A C = B D$ ，AC与BD相交于点O.

(1)、求证： $Δ A B C ≅ Δ D C B$ ；

(2)、 $Δ O B C$ 是何种三角形？

查看试题解析
23. 如图，在一块边长为 $a c m$ 的正方形纸片的四角，各剪去一个边长为 $b c m$ 的正方形，求剩余部分的面积.如果 $a = 3.6 ， b = 0.8$ 呢？.

查看试题解析
24. 某单位在疫情期间用 $3000$ 元购进 $A ， B$ 两种口罩 $1100$ 个，购买 $A$ 种口罩与购买 $B$ 种口罩的费用相同，且 $A$ 种口罩的单价是 $B$ 种口罩单价的 $1.2$ 倍.

(1)、求 $A ， B$ 两种口罩的单价各是多少元？

(2)、若计划用不超过 $7000$ 元的资金再次购进 $A ， B$ 两种口罩共 $2600$ 个，已知 $A ， B$ 两种口罩的进价不变，求 $A$ 种口罩最多能购买多少个？

查看试题解析
25. 如图，在等边 $Δ A B C$ 中， $A B = A C = B C = 10$ 厘米， $D C = 4$ 厘米，如果点 $M$ 以 $3$ 厘米 $/$ 的速度运动．

(1)、如果点 $M$ 在线段 $C B$ 上由点 $C$ 向点 $B$ 运动．点 $N$ 在线段 $B A$ 上由 $B$ 点向 $A$ 点运动，它们同时出发，若点 $N$ 的运动速度与点 $M$ 的运动速度相等：
①经过2秒后， $Δ B M N$ 和 $Δ C D M$ 是否全等？请说明理由．

②当两点的运动时间为多少秒时， $Δ B M N$ 刚好是一个直角三角形？

(2)、若点 $N$ 的运动速度与点 $M$ 的运动速度不相等，点 $N$ 从点 $B$ 出发，点 $M$ 以原来的运动速度从点 $C$ 同时出发，都顺时针沿 $Δ A B C$ 三边运动，经过 $25$ 秒时点 $M$ 与点 $N$ 第一次相遇，则点 $N$ 的运动速度是厘米 $/$ 秒．（直接写出答案）

查看试题解析