初中数学北师大版九年级下学期 第三章 3.3 垂径定理
试卷更新日期：2021-02-20 类型：同步测试
一、单选题
-
1. 如图，⊙O的弦AB＝16，M是AB的中点，且OM＝6，则⊙O的直径等于（ ）
A、12 B、16 C、20 D、242. 如图，在⊙O中，直径EF⊥CD，垂足为M，若CD=2 ，EM=5，则⊙O的半径为（ ）
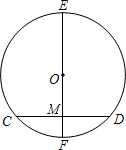A、2 B、3 C、4 D、63. 一条排水管的截面如图所示，已知排水管的半径 ，水面宽 ，则截面圆心 到水面的距离 是（ ）
A、2 B、3 C、 D、2.54. 如图是一个半径为5cm的圆柱形输油管的横截面，若油面宽AB=8cm，则油面的深度为（ ）
A、2cm B、2.5cm C、3cm D、3.5cm5. 如图，在⊙O中，弦AB长6cm，圆心O到AB的距离是3cm，⊙O的半径是（ ）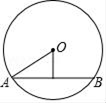
A、3cm B、3 cm C、4cm D、3 cm6. 已知⊙O的直径为10，圆心O到弦AB的距离OM为3，则弦AB的长是（ ）A、4 B、6 C、7 D、87. 如图，⊙O的直径AB=10，CD是⊙O的弦，CD⊥AB，垂足为E，且BE：AE=1：4，则CD的长为（ ）
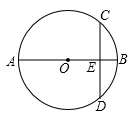A、10 B、12 C、8 D、98. 如图，在⊙O中，半径r＝10，弦AB＝16，P是弦AB上的动点（不含端点A，B），若线段OP长为正整数，则点P的个数有（ ）
A、4个 B、5个 C、6个 D、7个二、填空题
-
9. 如下图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C和D两点，AB＝10cm，CD＝6cm，则AC长为cm.
10. 如图，AB为圆O的弦，OC⊥AB，垂足为E，如果CE=2 ，AB=8 ，则圆O的半径为 ．
11. 运动会上，小捷掷出的铅球在场地上砸出一个小坑（图示是其主视图），其中AB为8cm，小坑的最大深度为3cm，则该铅球的半径为cm．
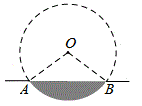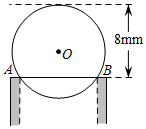
12. 如图，AB是 的直径，弦 于点E， ， ，则 cm.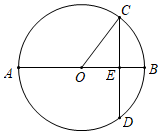
13. 工程上常用钢珠来测量零件口宽，假设钢珠的直径是10mm，测得钢珠的顶端离零件表面的距离为8mm，如图所示，则这个零件的口宽AB的长度是
三、解答题
-
14. ⊙O的半径为5cm，弦AB=6cm，CD=8cm，且AB∥CD，求两弦之间的距离.15. 往直径为 的圆柱形油槽内装入一些油以后，截面如图所示，若油面宽 ，求油的最大深度．
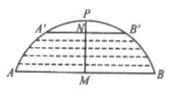
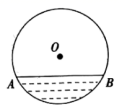16. 如图，在一座圆弧形拱桥，它的跨度AB为60m，拱高PM为18m，当洪水泛滥到跨度只有30m时，就要采取紧急措施，若某次洪水中，拱顶离水面只有4m，即PN=4m时，试通过计算说明是否需要采取紧急措施。
