浙江省杭州市萧山区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-02-20 类型：期末考试

进入出卷网下载

一、选择题(每题3分,共30分)

1. 16的平方根是（）

A、16 B、-4 C、±4 D、没有平方根

查看试题解析
2. 中国人民解放军的武器库中有一款高超音速导弹——东风17导弹，它是世界首款采用了“乘波体”的飞行器，其速度为20马赫左右，也就是秒速达到大约6850米。数6850用科学记数法可以表示为（）

A、685×10¹ B、68.5×10² C、6.85×10² D、6.85×10³

查看试题解析
3. 下图中标注的角可以用∠O来表示的是（）

A、 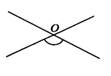B、 C、 D、

查看试题解析
4. -2021的绝对值和相反数分别为（）

A、2021， -2021 B、-2021，2021 C、2021，2021 D、-2021，-2021

查看试题解析
5. 下列说法正确的是（）

A、单项式3ab的次数是1 B、3a－2a $^{2}$ b+2ab是三次三项式 C、单项式 $\frac{2 a b}{3}$ 的系数是2 D、－4a $^{2}$ b，3ab ， 5是多项式－4a $^{2}$ b+3ab-5的项

查看试题解析
6. 估计 $\sqrt{13}$ +3的值在（）

A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间

查看试题解析
7. 下列各组式子中，是同类项的是（）

A、3x²y与-3xy² B、3xy与-2yx C、3x与3x² D、3xy与3yz

查看试题解析
8. 今年父亲的年龄是儿子的5倍，5年前父亲的年龄是儿子的15倍，设今年儿子的年龄为x，可得方程（）

A、5x-5=15(x-5) B、5x+5=15(x-5) C、5x-5=15(x+5) D、5x+5=15(x+5)

查看试题解析
9. 已知：x-3y=4，那么代数式 $x - 3 y - 3 (y - x) - 2 (x - 3)$ 的值为（）

A、12 B、13 C、14 D、16

查看试题解析
10. 如图，点A，B，C是直线 $l$ 上的三个定点，AB=3BC，AB-BC=6 m，其中m为大于0的常数，若点D是直线 $l$ 上的一动点，M、N分别是AD、CD的中点，则MN与BC的数量关系是（）

A、MN=2BC B、MN=BC C、MN=3BC D、2MN=3BC

查看试题解析

二、填空题(每题4分,共24分)

11. 在1，-3，0，-2四个数中，最小的数是.

查看试题解析
12. 把式子 $\frac{5}{3} \times \frac{5}{3} \times \frac{5}{3} \times \frac{5}{3} \times \frac{5}{3}$ 写成乘方的形式为.

查看试题解析
13. 已知 $- \frac{1}{4} a^{2} b^{m} c$ 是一个5次单项式，则式子3m²-6m+1的值是.

查看试题解析
14. 一个边长为a的正方形的面积为 $\frac{16}{49}$ ，一个棱长为b的立方体的体积为 $\frac{343}{8}$ ，则 $\sqrt{a b}$ =.

查看试题解析
15. 已知关于x的方程x＋2－ $\frac{1}{2021}$ x=m的解是x=21,那么关于y的一元一次方程y＋23－ $\frac{1}{2021}$ （y＋21）=m的解是y=.

查看试题解析
16. 将一张纸如图所示折叠后压平，点F在线段BC上，EF、GF为两条折痕，若∠1=51°，∠2=20°，∠3的度数.

查看试题解析

三、解答题（共66分）

17. 计算：

(1)、13 $\frac{3}{4}$ ＋(－0.25)－(－ $4 \frac{1}{4}$ )＋ $| - 3 - \frac{1}{4} |$

(2)、(-2)³－9÷ $\frac{1}{3}$

(3)、 $- 100 \frac{1}{4} \times 4$ -66（ $\frac{1}{6}$ － $\frac{2}{3} \times \frac{5}{11}$ ）

查看试题解析
18. 解方程：

(1)、3(x-2)+8x=5

(2)、 $\frac{x - 2}{3} - 0.5 = \frac{5 x}{6}$

查看试题解析
19. 已知点直线BC及直线外一点A(如图），按要求完成下列问题：

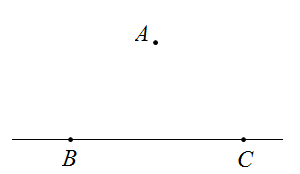(1)、画出射线CA、线段AB.过C点画CD⊥AB，垂足为点D；

(2)、比较线段CD和线段CA的大小，并说明理由；

(3)、在以上的图中，互余的角为，互补的角为.（各写出一对即可）

查看试题解析
20. 植树节，小明种树的棵数是小聪的1.5倍，小慧种树的棵数比小明少8棵.

(1)、设小明种了x棵，问他们三人一共种了多少棵树？（用含x的代数式表示）

(2)、若小聪发现他比小慧多种的棵树等于他比小明少种的棵树，他们三人一共种了多少棵树?

查看试题解析
21. 如图，已知直线AB，CD相交于点O，OE，OF为射线，∠AOE=90°，OF平分∠BOC

(1)、若∠EOF=30°，求∠BOD的度数；

(2)、试问∠EOF与∠BOD有什么数量关系？请说明理由.

查看试题解析
22. 若化简代数式 $(x^{3} + \frac{1}{3} b x^{2} - 5 x - 1) - (2 a x^{3} - x^{2} + x - 5)$ 的结果中不含 $x^{2}$ 和 $x^{3}$ 项，

(1)、试求a，b的值；

(2)、在（1）的条件下，求整式3a²b－ab²的5倍与ab²+3a²b的差.

查看试题解析
23. 数轴上A点对应的数为－10,B点在A点右边，甲、乙在B分别以2个单位／秒、1个单位／秒的速度向左运动，丙在A以3个单位／秒的速度向右运动.

(1)、若它们同时出发，经过5秒丙和乙相遇，求B点表示的数；

(2)、在(1)的条件下，设它们同时出发的时间为t秒，是否存在t(t>0)的值，使得甲、乙、丙三个点中的其中一个点，到另外两个点的距离相等。

查看试题解析