浙江省湖州市南浔区2021届九年级上学期数学期末考试试卷
试卷更新日期：2021-02-20 类型：期末考试
一、选择题(本题有 10 小题，每小题 3 分，共 30 分)
-
1. 已知⊙O 的半径为 8cm，如果一点P和圆心 O 的距离为 8cm，那么点 P 与⊙O 的位置关系是（ ）A、点 P 在⊙O 内 B、点 P 在⊙O 上 C、点 P 在⊙O 外 D、不能确定2. 下列说法正确的是（ ）A、抛掷一枚质地均匀的硬币两次，必有一次正面朝上 B、“汽车累积行驶 10000km，从未出现故障”是不可能事件 C、湖州气象局预报说“明天的降水概率为 70%”，意味着湖州明天一定下雨 D、“|a|＞0”是必然事件3. 抛物线 y＝x2＋2x＋2 与 y 轴的交点坐标为（ ）A、(1，0) B、(0，1) C、(0，0) D、(0，2)4. 生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下a与全身 的高度比值接近0.618，可以增加视觉美感，若图中 为2米，则a约为（ ）
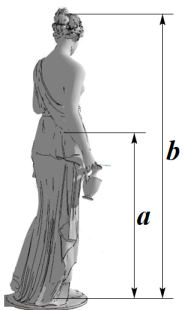A、1.24米 B、1.38米 C、1.42米 D、1.62米5. 如图，已知在平行四边形 ABCD 中，E 为 CD 上一点，连结 AE ， BD ， 且 AE ， BD 交于点 F ， S△DEF ： S△ABF = 4 ： 25 ，则 DE：AB 的值是（ ）
A、2：5 B、2：3 C、3：5 D、3：26. 已知，在 Rt△ABC 中，∠C＝90°，BC＝3，AC＝4，则 sinA 的值是（ ）A、 B、 C、 D、7. 如图，已知⊙O 的直径 CD＝8，AB 是⊙O 的弦，AB⊥CD ， 垂足为 M ， OM＝2，则 AB 的长为（ ）
A、2 B、2 C、4 D、48. 如图，点 A ， B ， C ， D 为⊙O 上的四个点，AC 平分∠BAD ， AC 交 BD 于点 E ， CE＝4，CD＝6， 则 AC 的长为( )
A、7 B、8 C、9 D、109. 已知二次函数 y = a(x - x1)(x - x2 ) 与 x 轴的交点是(1，0)和(3，0)，关于 x 的方程a(x - x1)(x - x2 ) = m(其中 m＞0)的两个解分别是－1 和 5，关于 x 的方程 a(x -x1)(x - x2 ) = n (其中 0＜n＜m)也有两个整数解，这两个整数解分别是（ ）A、1 和 4 B、2 和 5 C、0 和 4 D、0 和 510. 如图，已知在 Rt△ABC 中，∠ACB＝90°，AC＝3，BC＝4，以 AB 为直径向外作半圆 O ， P 是半圆 O上的一个动点，M 是 CP 的中点，当点 P 沿半圆 O 从点 A 运动至点 B 时，点 M 的运动路径长为（ ）
A、π B、π C、2π D、 π二、填空题(本题有 6 小题，每小题 4 分，共 24 分)
-
11. 抛物线 y＝3(x－1)2＋8 的顶点坐标为.12. 已知一条弧所对的圆心角为 80°，则这条弧所对的圆周角度数为°.13. 一个不透明的袋中装有除颜色外其余均相同的 1 个红球和 2 个黄球，从中随机摸出一个，则摸到红球的概率 P＝.14. 如图，已知在△ABC 中，BC＝120，高 AD＝60，正方形 EFGH 一边在 BC 上，点 E ， F 分别在 AB ， AC 上，AD 交 EF 于点 N ， 则 AN 的长为.
15. 如图是我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由四个全等的直角三角形与二个正方形拼成的．如果大正方形的面积是 125，小正方形面积是 25，则 cosθ 的值为.
16. “水晶晶南浔”的美食文化中以特有的双交面出名，盛面的瓷碗截面图如图 1 所示，碗体 DEC 呈抛物线状(碗体厚度不计)，点 E 是抛物线的顶点，碗底高 EF＝1cm，碗底宽 AB＝2 cm，当瓷碗中装满面汤时，液面宽 CD＝83cm，此时面汤最大深度 EG＝6cm，将瓷碗绕点 B 缓缓倾斜倒出部分面汤，如图2，当 LABK＝30 时停止，此时液面 CH 到桌面的距离为cm；碗内面汤的最大深度是cm．
三、解答题(本题有 8 小题，共 66 分)
-
17. 计算：tan45°＋ cos30°．18. 如图的方格地面上，标有编号 A、B、C 的 3 个小方格地面是空地，另外 6 个小方格地面是草坪，除此以外小方格地面定全相同．
(1)、一只自由飞行的小鸟，将随意地落在图中的方格地面上，问小鸟落在草坪上的概率是多少?(2)、现从 3 个小方格空地中任意选取 2 个种植草坪，则刚好选取 A 和 B 两个小方格空地种植草坪的概率是多少?(用树形图或列表法求解)19. 如图，已知在平面直角坐标系 xOy 中，二次函数 y＝ax2－4x＋5 的图象顶点为 A ， 与 x 轴交于点 B 和点 C ， 与 y 轴交于点 D．点 A 的横坐标是－2．
(1)、求 B ， C 两点的坐标；(2)、平移该二次函数的图象使点 A 恰好落在点 D 的位置上，求平移后图象所对应的二次函数的表达式．20. 根据新冠疫情的防疫需要，学校需要做到经常开窗通风．如图 1，一扇窗户打开一定角度，其中一端固定在窗户边 OM 上的点 A 处，另一端 B 在边ON 上滑动，如图 2 为某一位置从上往下看的平面图， 测得此时∠ABO 是 45°，AB 长为 20cm．(参考数据； sin 37°» 0.6，cos 37°» 0.8，tan 37°» 0.75， » 1.4 ，结果精确到 1cm)
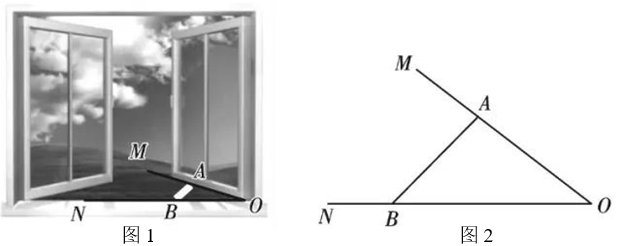(1)、求固定点 A 到窗框 OB 的距离；(2)、若测得∠AOB＝37°，求 OA 的长度．21. 如图，已知由边长为 1 的小等边三角形构成的网格中，每个小等边三角形的顶点称为格点，以格点为顶点的三角形叫格点三角形，△ABC 为格点三角形．请仅用无刻度直尺在网格中完成下列画图．
(1)、画出△ABC 绕点 A 顺时针旋转 60°后得到的△AB'C'；(2)、在 BC 边上找一点 D ， 连结 AD ， 使得△ABD 的面积与△ACD 的面积之比是 2：1．(温馨提示：请画在答题卷相对应的图上)22. 近期多次出现进口冷冻牛肉外包装新冠病毒核酸呈阳性，国内的新鲜牛肉价格出现了大幅度涨价.某牛肉摊位购进一批国产新鲜牛肉，进价为每千克 40 元，物价部门规定其销售价不低于成本价且不高于成本价的 2 倍．经试销发现，日销售量 y(千克)与销售单价 x(元/千克)符合如图所示的一次函数关系：
(1)、求 y 与 x 的函数关系式，并写出自变量 x 的取值范围；(2)、若在销售过租中每天还要支付其他费用 300 元，当销售单价为多少时，该批国产新鲜牛肉的日获利最大?最大获利是多少元?23. 已知抛物线 y＝－x2＋bx＋c(a≠0)与 y 轴交于点 A ， 点 B( ， 2)在该抛物线上
(1)、若抛物线的对称轴是直线 x＝m ， 请用含 b 的式子表示 m；(2)、如图 1．过点 B 作 x 轴的垂线段，垂足为点 C．连结 AB 和 AC ， 当△ABC 为等边三角形时，求抛物线解析式；(3)、如图 2，在(2)条件下，已知 P 为 x 轴上的一动点，连结 AP 和 BP ， 当∠APB＝30°时，求满足条件的点 P 的坐标．24. 【概念认识】定义：对角线互相垂直且相等的四边形叫做垂等四边形．
(1)、如图 1，已知在垂等四边形 ABCD 中，对角线 AC 与 BD 交于点 E ， 若 AB⊥AD ， AB＝4cm，cos∠ABD= 求 AC 的长度，(2)、【数学理解】在探究如何画“圆内接垂等四边形”的活动中，小李与同学讨论出了如下方法：如图 2，在⊙O 中，已知 AB 是⊙O 的弦，只需作 OD⊥OA、OC⊥OB ， 分别交⊙O 于点 D 和点 C ， 即可得到垂等四边形 ABCD ， 请你写出证明过程．
(3)、【问题解决】如图 3，已知 A 是⊙O 上一定点，B 为⊙O 上一动点，以 AB 为一边作出⊙O 的内接垂等四边形(A、B 不重合且 A、B、0 三点不共线)，对角线 AC 与 BD 交于点 E ， ⊙O 的半径为 2 ，当点 E 到 AD 的距离为 时，求弦 AB 的长度．