四川省资阳市2020-2021学年高二上学期文数期末考试试卷

试卷更新日期：2021-02-19 类型：期末考试

进入出卷网下载

一、单选题

1. 已知P椭圆 $\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$ 上的动点，则P到该椭圆两焦点的距离之和为（）

A、 $2 \sqrt{3}$ B、4 C、 $4 \sqrt{3}$ D、8

查看试题解析
2. 已知命题 $p : \forall x \in R$ ， $e^{x} \geq x + 1$ ，则 $\neg p$ 为（）

A、 $\forall x \in R$ ， $e^{x} < x + 1$ B、 $\exists x_{0} \in R$ ， $e^{x_{0}} \geq x_{0} + 1$ C、 $\exists x_{0} \in R$ ， $e^{x_{0}} \leq x_{0} + 1$ D、 $\exists x_{0} \in R$ ， $e^{x_{0}} < x_{0} + 1$

查看试题解析
3. 在区间 $[- 3 ， 4]$ 上任取一个实数，则 $| x | \leq 1$ 的概率为（）

A、 $\frac{1}{7}$ B、 $\frac{6}{7}$ C、 $\frac{2}{7}$ D、 $\frac{5}{7}$

查看试题解析
4. 已知 $x ， y \in R$ ，则“ $\ln x = \ln y$ ”是“ $x = y$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、即不充分也不必要条件

查看试题解析
5. 执行如图所示的程序框图，若输入的 $x$ 为-4，则输出 $y$ 的值为（）

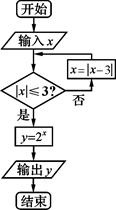A、0.5 B、1 C、2 D、4

查看试题解析
6. 我市创建省级文明城市，需要每一位市民的支持和参与.为让全年级1000名同学更好的了解创建文明城市的重大意义，学校用系统抽样法(按等距的原则)从高二年级抽取40名同学对全年级各班进行宣讲，将学生从 $1$ ~1000进行编号，现已知第1组抽取的号码为13，则第5组抽取的号码为（）

A、88 B、113 C、138 D、173

查看试题解析
7. 某商铺统计了今年5个月的用电量y(单位：10kw/h)与月份x的对应数据，列表如下：

x

2

4

5

6

8

y

30

40

57

a

69

根据表中数据求出 $y$ 关于 $x$ 的线性回归方程为 $\hat{y} = 6.5 x + 17.5$ ，则上表中 $a$ 的值为（）

A、50 B、54 C、56.5 D、64

查看试题解析
8. 若圆 ${(x - 1)}^{2} + {(y - 3)}^{2} = 4$ 与圆 ${(x + 2)}^{2} + {(y + 1)}^{2} = a + 5$ 外切，则 $a =$ （）

A、-4 B、-1 C、4 D、11

查看试题解析
9. 若圆心在x轴上，半径为2的圆C位于y轴左侧，且与直线 $2 x + y = 0$ 相切，则圆C的方程是（）

A、 ${(x - \sqrt{5})}^{2} + y^{2} = 4$ B、 ${(x + \sqrt{5})}^{2} + y^{2} = 4$ C、 ${(x - 5)}^{2} + y^{2} = 4$ D、 ${(x + 5)}^{2} + y^{2} = 4$

查看试题解析
10. 已知m，n为两条不同的直线， $α / / β$ 是两个不同的平面，下列命题为真命题的是（）

A、 $m ⊥ n, m / / α \Rightarrow n ⊥ α$ B、 $n / / β, β ⊥ α \Rightarrow n ⊥ α$ C、 $m / / n, m ⊥ β \Rightarrow n ⊥ β$ D、 $m / / α, n \subset α \Rightarrow m / / n$

查看试题解析
11. 过椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左顶点A作圆 $x^{2} + y^{2} = c^{2}$ (2c是椭圆的焦距)两条切线，切点分别为M，N，若∠MAN=60°，则该椭圆的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
12. 如图，棱长为3的正方体ABCD-A₁B₁C₁D₁中，P为正方体表面BCC₁B₁上的一个动点，E，F分别为BD₁的三等分点，则 $| P E | + | P F |$ 的最小值为（）

A、 $3 \sqrt{3}$ B、 $\frac{5 \sqrt{2}}{2}$ C、 $1 + \sqrt{6}$ D、 $\sqrt{11}$

查看试题解析

二、填空题

13. 椭圆 $\frac{x^{2}}{8} + \frac{y^{2}}{4} = 1$ 的右焦点坐标为.

查看试题解析
14. 某几何体的三视图如图所示，则该几何体的体积为.

查看试题解析
15. 把一枚质地均匀的骰子投掷两次，第一次出现的点数为m，第二次出现的点数为n，设事件A为方程组 ${\begin{array}{l} m x + n y = 5 \\ x^{2} + y^{2} = 1 \end{array}$ 有唯一解，则事件A发生的概率为.

查看试题解析
16. 若M，P是椭圆 $\frac{x^{2}}{4} + y^{2} = 1$ 两动点，点M关于x轴的对称点为N，若直线PM，PN分别与x轴相交于不同的两点A(m，0)，B(n，0)，则mn=.

查看试题解析

三、解答题

17. 命题p：曲线 $x^{2} + y^{2} + 2 m x - 2 m y + 8 = 0$ 表示一个圆；命题q：指数函数 $f (x) = {(2 m - 1)}^{x}$ 在定义域内为单调递增函数.

(1)、若 $p$ 为真命题，求实数 $m$ 的取值范围；

(2)、若 $p \lor q$ 为真， $p \land q$ 为假，求实数 $m$ 的取值范围.

查看试题解析
18. 已知曲线C： $\frac{x^{2}}{a} + \frac{y^{2}}{b} = 1 (a > 0 ， b > 0)$ ，集合 $A = {1 ， 2 ， 3 ， 4}$ ， $B = {1 ， 2 ， 3}$ .

(1)、若 $a ， b \in B$ ，求曲线C为半径 $r \geq \sqrt{2}$ 的圆的概率；

(2)、若 $a \in A ， b \in B$ ，求曲线C为焦点在x轴上的椭圆的概率.

查看试题解析
19. 已知点P(-1，4)，Q(3，2).

(1)、求以PQ为直径的圆N的标准方程；

(2)、过点M(0，2)作直线l与（1）中的圆N相交于A，B两点，若 $| A B | = 4$ ，求直线l的方程.

查看试题解析
20. 某次数学测试后，数学老师对该班n位同学的成绩进行分析，全班同学的成绩都分布在区间 $[95 ， 145]$ ，制成的频率分布直方图如图所示.已知成绩在区间 $[125 ， 135)$ 的有12人.

(1)、求n；

(2)、根据频率分布直方图，估计本次测试该班的数学平均分(同一组数据用该组数据区间的中点值表示).

(3)、现从 $[125 ， 135)$ ， $[135 ， 145]$ 两个分数段的试卷中，按分层抽样的方法共抽取了6份试卷.若从这6份试卷中随机选出2份作为优秀试卷，求选出2份优秀试卷中恰有1份分数在 $[135 ， 145]$ 的概率.

查看试题解析
21. 如图，四棱锥 $S - A B C D$ 的底面是正方形， $S D ⊥$ 平面 $A B C D$ ， $S D = 2$ ， $A D = \sqrt{2}$ ，点 $E$ 是线段 $S D$ 上的点，且 $D E = a (0 < a \leq 2)$ .

(1)、求证：对任意的 $0 < a \leq 2$ ，都有 $A C ⊥ B E$ ；

(2)、当 $a = 1$ 时，点 $M$ 是 $S C$ 上的点，且 $S M = 2 M C$ ，求三棱锥 $E - B C M$ 的体积.

查看试题解析
22. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 右焦点 $F (1 ， 0)$ ， $A, B$ 是分别为椭圆 $C$ 的左､右顶点， $P$ 为椭圆的上顶点，三角形 $P A B$ 的面积 $S = \sqrt{2}$ .

(1)、求椭圆 $C$ 的方程；

(2)、直线 $l ： y = x + m$ 与椭圆交于不同的两点 $M, N$ ，点 $Q (2 ， 0)$ ，若 $∠ M Q O = ∠ N Q O$ ( $O$ 是坐标原点)，求 $m$ 的值.

查看试题解析