湖北省新高考联考协作体2020-2021学年高二上学期数学期末考试试卷
试卷更新日期:2021-02-19 类型:期末考试
一、单选题
-
1. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,2. 已知i为虚数单位,且复数 ,则复数z的共轭复数为( )A、 B、 C、 D、3. 已知双曲线的: 的实轴长为虚轴长的3倍,则双曲线的离心率e为( )A、 B、 C、 D、4. 已知x与y之间的一组数据如下表:
x
3
4
5
6
y
30
40
60
50
若y与x线性相关,根据上表求得y与x的线性回归方程, 中的 为8,据此模型预报 时y的值为( )
A、70 B、63 C、65 D、665. 已知m,n是两条不同的直线, , 是两个不同的平面,则下列命题中正确的是( )A、若 , , ,则 . B、若 , ,则 . C、若 , , ,则 . D、若 , , , ,则 .6. 在三棱柱 中,侧棱垂直于底面, , , , ,点E为 的中点,点F在 的延长线上且 ,则异面直线 与 所成的角为( ) A、90° B、60° C、45° D、30°7. 皮埃尔·德·费马,法国律师和业余数学家,被誉为“业余数学家之王”,对数学作出了重大贡献,其中在1636年发现了:若p是质数,且a,p互质,那么a的 次方除以p的余数恒等于1,后来人们称该定理为费马小定理.依此定理若在数集 中任取两个数,其中一个作为p,另一个作为a,则所取两个数符合费马小定理的概率为( )A、 B、 C、 D、8. 已知 的图象如图所示,其中 是函数 的导数,则所给选项的四个图象中,函数 的图象可能是( )
A、90° B、60° C、45° D、30°7. 皮埃尔·德·费马,法国律师和业余数学家,被誉为“业余数学家之王”,对数学作出了重大贡献,其中在1636年发现了:若p是质数,且a,p互质,那么a的 次方除以p的余数恒等于1,后来人们称该定理为费马小定理.依此定理若在数集 中任取两个数,其中一个作为p,另一个作为a,则所取两个数符合费马小定理的概率为( )A、 B、 C、 D、8. 已知 的图象如图所示,其中 是函数 的导数,则所给选项的四个图象中,函数 的图象可能是( ) A、
A、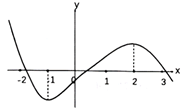 B、
B、 C、
C、 D、
D、
二、多选题
-
9. 已知函数 , ,则下列说法正确的有( )A、 是奇函数 B、 是周期函数 C、曲线 在点 处的切线方程为 D、在区间 上, 单调递增10. 下列说法正确的是( )A、向量 , ,且 与 共线,则实数k为-2 B、“ ”是“ ”的必要不充分条件 C、“ ”是“ ”的充要条件 D、对于命题“ , ”是真命题,则实数a的取值范围是11. 已知 , 是椭圆 的两个焦点,过 的直线l与椭圆C交于A,B两点,O为坐标原点,则下列说法正确的是( )A、椭圆C的离心率为 B、存在点A使得 C、若 ,则 D、 面积的最大值为1212. 如图,点M是棱长为2的正方体 中的线段 上的一个动点,则下列结论正确的是( )
 A、存在点M,使 平面 B、不存在点M满足 C、存在点M,使异面直线 与 所成的角是60° D、二面角 的正弦值为
A、存在点M,使 平面 B、不存在点M满足 C、存在点M,使异面直线 与 所成的角是60° D、二面角 的正弦值为三、填空题
-
13. 已知向量 , ,且 与 互相垂直,则 .14. 用长为24 的钢条围成一个长方体框架,要求长方体的长与宽之比为3 1,则长方体的宽为时,其体积最大.15. 抛物线 的焦点为F,准线为l,经过点F的斜率为 的直线 交抛物线于A,B两点,交点B在x轴的下方, ,垂足为点 ,则 的面积为.16. 已知 是定义在 上的奇函数, ,且当 时 ,则不等式 的解集是.
四、解答题
-
17. 已知函数 .(1)、求曲线 在点 处的切线的方程;(2)、求函数 的极值.18. 在①平面 平面 , ;② , ;③ 平面 , .这三个条件中任选一个,补充在下面的问题中并作答.
如图,在四棱柱 中,底面 是梯形,点E在 上, , , ,且 ▲ .
 (1)、求证:平面 平面 ;(2)、求直线 与平面 所成的角的正弦值.19. 已知抛物线 ,焦点为F,过点 作直线l交抛物线于A,B两点.
(1)、求证:平面 平面 ;(2)、求直线 与平面 所成的角的正弦值.19. 已知抛物线 ,焦点为F,过点 作直线l交抛物线于A,B两点. (1)、证明: 为定值(O为原点, , 为直线 , 的斜率);(2)、求三角形 的面积 的最小值.20. 某中学举行了一次“环保知识竞赛”活动,为了解本次竞赛的学生成绩情况,从中随机抽取了 名学生的成绩(假设竞赛成绩均在 内)作为样本进行统计.按照 , , , , 分为五组作出了如下频率分布直方图,并列出了分数在 和 的茎叶图.
(1)、证明: 为定值(O为原点, , 为直线 , 的斜率);(2)、求三角形 的面积 的最小值.20. 某中学举行了一次“环保知识竞赛”活动,为了解本次竞赛的学生成绩情况,从中随机抽取了 名学生的成绩(假设竞赛成绩均在 内)作为样本进行统计.按照 , , , , 分为五组作出了如下频率分布直方图,并列出了分数在 和 的茎叶图. (1)、由图中数据求出 , , 的值;(2)、若从竞赛成绩在 , , 的学生中用分层抽样的方法抽取6名学生组成环保知识宣传小组,定期在校内进行义务宣传,并在这6名学生中随机抽取2名学生参加市组织的环保知识竞赛,求竞赛成绩在 内的学生至少有1名学生被抽到的概率.
(1)、由图中数据求出 , , 的值;(2)、若从竞赛成绩在 , , 的学生中用分层抽样的方法抽取6名学生组成环保知识宣传小组,定期在校内进行义务宣传,并在这6名学生中随机抽取2名学生参加市组织的环保知识竞赛,求竞赛成绩在 内的学生至少有1名学生被抽到的概率.
