湖北省黄冈市2020-2021学年高二上学期数学期末考试试卷

试卷更新日期：2021-02-19 类型：期末考试

进入出卷网下载

一、单选题

1. 晓霞在学校的“经典诗词朗诵”大赛中，5位评委给她的分数分别是：93，93，95，96，92，则晓霞得分的中位数与平均数分别是（）

A、93；93 B、93；93.8 C、93.5；93.5 D、94；93.8

查看试题解析
2. 已知向量 $\vec{a} = (2, 1, 3)$ ， $\vec{b} = (x, 2, 1 - x)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $x =$ （）

A、-5 B、5 C、4 D、-1

查看试题解析
3. 马克吐温是美国著名的幽默讽刺作家，他的小说揭露和讽刺了美国社会的一些黑暗现象．他曾痛骂美国国会“有些议员是笨蛋”，因此被要求道歉，否则被控告诽谤罪．于是马克吐温登报表示歉意并纠正道：美国国会“有些议员不是笨蛋”．请问“有些议员不是笨蛋”的否定是（）

A、有些议员是笨蛋 B、每个议员都是笨蛋 C、每个议员都不是笨蛋 D、有些议员不是笨蛋

查看试题解析
4. 已知圆 $C_{1} : x^{2} + y^{2} - 2 x + 12 y + 33 = 0$ 与圆 $C_{2} : x^{2} + y^{2} + 10 x - 4 y - 52 = 0$ ，则两圆公切线条数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 设随机变量 $ξ$ 服从正态分布 $N (μ, σ^{2})$ ，函数 $f (x) = x^{2} + 4 x + ξ$ 没有零点的概率是 $\frac{1}{2}$ ，则 $μ$ 等于（）

A、1 B、2 C、4 D、不能确定

查看试题解析
6. 已知二项式 ${(2 x - 1)}^{n}$ 的展开式中仅有第4项的二项式系数最大，则展开式中 $x^{3}$ 项的系数为（）

A、-80 B、80 C、-160 D、-120

查看试题解析
7. 已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = A C = \frac{1}{2} A A_{1} = 1$ ， $∠ A_{1} A C = ∠ A_{1} A B = \frac{π}{3}$ ，D点是线段 $A B$ 上靠近A的一个三等分点，则 $\vec{C D} \cdot \vec{B_{1} B} =$ （）

A、 $\frac{2}{3}$ B、 $- \frac{2}{3}$ C、 $\frac{4}{3}$ D、 $- \frac{4}{3}$

查看试题解析
8. 学校举行秋季运动会，高一（1）班选出5名同学参加跳高、跳远、跳绳三个项目比赛，每个项目至少有一名同学参加，则甲不参加跳绳比赛的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{12}{25}$ C、 $\frac{31}{60}$ D、 $\frac{2}{3}$

查看试题解析

二、多选题

9. 下列命题中正确的有（）

A、对立事件一定是互斥事件，但互斥事件不一定是对立事件 B、两个随机变量的线性相关系数越大，则两个变量的线性相关性越强 C、回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 必过样本点的中心 D、相关指数 $R^{2}$ 越大，则模型的拟合效果越好

查看试题解析
10. 已知直线 $l : a x - y - 3 a = 0$ 上存在相距为4的两个动点A，B，若圆 $C : {(x + 1)}^{2} + {(y - 4)}^{2} = 4$ 上存在点P使得 $△ P A B$ 是以点P为直角顶点的等腰直角三角形，则实数a的值可以为（）

A、-2 B、-1 C、0 D、1

查看试题解析
11. 已知球O为正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的内切球，平面 $A_{1} C_{1} B$ 截球O的面积为 $24 π$ ，下列命题中正确的有（）

A、异面直线 $A C$ 与 $B C_{1}$ 所成的角为60° B、 $B D_{1} ⊥$ 平面 $A_{1} C_{1} B$ C、球O的表面积为 $36 π$ D、三棱锥 $B_{1} - A_{1} C_{1} B$ 的体积为288

查看试题解析
12. 为弘扬我国古代“六艺”文化，某研学旅行夏令营主办单位计划在暑假开设“礼、乐、射、御、书、数”六门体验课程，若甲乙丙三名同学各只能体验其中一门课程．则（）

A、甲乙丙三人选择课程方案有 $120$ 种方法 B、恰有三门课程没有被三名同学选中的概率为 $\frac{5}{9}$ C、已知甲不选择课程“御”的条件下，乙丙也不选择“御”的概率为 $\frac{25}{36}$ D、设三名同学选择课程“礼”的人数为 $ξ$ ，则 $E ξ = \frac{1}{2}$

查看试题解析

三、填空题

13. 若数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ，…， $x_{n}$ 的方差为3，则数据 $3 x_{1} - 2$ ， $3 x_{2} - 2$ ， $3 x_{3} - 2$ ，…， $3 x_{n} - 2$ 的方差为．

查看试题解析
14. 若 ${(3 x + 2)}^{2020} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{2020} x^{2020}$ ，则 $a_{1} + a_{3} + a_{5} + \dots + a_{2019}$ 被12整除的余数为．

查看试题解析
15. 过点 $P (3 ， 4)$ 作圆 $x^{2} + y^{2} = 10$ 的两条切线，设切点分别为A，B，则线段 $A B =$ ．

查看试题解析
16. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 6$ ， $A C = 8$ ，D是斜边上一点，以 $A D$ 为棱折成60°二面角 $C - A D - B$ ，则线段 $B C$ 最小值为．

查看试题解析

四、解答题

17. 已知四棱锥 $P - A B C D$ 中底面 $A B C D$ 为菱形， $P A = P C$ ．

(1)、求证： $B C / /$ 平面 $P A D$ ；

(2)、求证： $P B ⊥ A C$ ．

查看试题解析

18. 为了解国内不同年龄段的民众旅游消费基本情况，某旅游网站从其数据库中随机抽取了1000条客户信息进行分析，这些客户一年的旅游消费金额如下表：

旅游消费（千元）	$[0 ， 2)$	$[2 ， 4)$	$[4 ， 6)$	$[6 ， 8)$	$[8 ， 10)$	$[10 ， + \infty)$	合计
年轻人（人）	90	80	70	60	60	40	400
中老年（人）	55	90	125	130	110	90	600

把一年旅游消费金额满8千元的称为“高消费”，否则称为“低消费”．

(1)、从这些客户中随机选一人，求该客户是“高消费”的年轻人的概率；

(2)、完成

2 \times 2

列联表，并判断能否有99%的把握认为旅游消费高低与年龄有关．

	低消费	高消费	合计
年轻人（人）
中老年（人）
合计

附： $2 \times 2$ 列联表参考公式： $k^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．

临界值表：

$P (K^{2} \geq k_{0})$	0.100	0.050	0.025	0.010	0.001
$k_{0}$	2.706	3.841	5.024	6.635	10.828

查看试题解析

19. 某班级60名学生的考试分数x分布在区间 $[90 ， 150]$ 内．设考试分数x的频率分布为 $f (x)$ ，且满足 $f (x) = {\begin{array}{l} \frac{n}{12} - \frac{2}{3} ， 10 n \leq x < 10 (n + 1) ， n = 9 ， 10 ， 11 \\ - \frac{n}{8} + t ， 10 n \leq x < 10 (n + 1) ， n = 12 ， 13 ， 14 \end{array}$ ，考试成绩采用“6分制”，规定：考试分数在区间 $[90 ， 100)$ ， $[100 ， 110)$ ， $[110 ， 120)$ ， $[120 ， 130)$ ， $[130 ， 140)$ ， $[140 ， 150]$ 内的成绩依次记为1分，2分，3分，4分，5分，6分．在60名学生中用分层抽样的方法从成绩为1，2，3分的学生中随机抽取6人，再在这6人中随机抽查3人，记这3人成绩之和为 $ξ$ ．

(1)、求t的值；

(2)、求 $ξ$ 的分布列及数学期望．

查看试题解析
20. 已知与 $x = - 1$ 相切的圆C的圆心在射线 $x - 3 y = 0 (x > 0)$ 上，且被直线 $l ： 3 x - 4 v + 5 = 0$ 截得弦长为 $4 \sqrt{3}$ ．

(1)、求圆C的方程；

(2)、若圆C上有且仅有2个点到与l平行的直线 $l^{'}$ 的距离为2，求直线 $l^{'}$ 在x轴上截距的取值范围．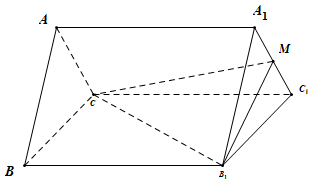

查看试题解析
21. 三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧面 $B B_{1} C_{1} C$ 为菱形， $∠ C B B_{1} = 60 °$ ， $A B ⊥ A C$ ， $A B = A C$ ， $B C = A B_{1} = 2$ ．

(1)、求证：面 $A B C ⊥$ 面 $B B_{1} C_{1} C$ ；

(2)、在线段 $C_{1} A_{1}$ 上是否存在一点M，使得二面角 $M - C B_{1} - C_{1}$ 为 $\frac{π}{6}$ ，若存在，求出 $\frac{C_{1} M}{C_{1} A_{1}}$ 的值，若不存在，请说明理由．

查看试题解析
22. 在某市举办的“中华文化艺术节”知识大赛中，大赛分预赛与复赛两个环节．预赛有4000人参赛．先从预赛学生中随机抽取100人成绩得到如下频率分布直方图：

(1)、若从上述样本中预赛成绩不低于60分的学生中随机抽取2人，求至少1人成绩不低于80分的概率；

(2)、由频率分布直方图可以认为该市全体参加预赛的学生成绩Z服从正态分布 $N (μ ， σ^{2})$ ，其中 $μ$ 可以近似为100名学生的预赛平均成绩， $σ^{2} = 362$ ，试估计全市参加预赛学生中成绩不低于91分的人数；

(3)、预赛成绩不低于91分的学生可以参加复赛．复赛规则如下：①每人复赛初始分均为100分；②参赛学生可在开始答题前自行选择答题数量 $n (n > 1)$ ，每答一题需要扣掉一定分数来获取答题资格，规定回答第 $k (k = 1 ， 2 ， \dots ， n)$ 题时扣掉 $0.2 k$ 分；③每答对一题加2分，答错既不加分也不扣分；④答完n题后参赛学生的最后分数即为复赛分数．已知学生甲答对每题的概率为0.75，且各题答对与否相互独立，若甲期望得到最佳复赛成绩，则他的答题数量n应为多少？
（参考数据 $\sqrt{362} \approx 19$ ，若 $z ~ N (μ ， σ^{2})$ ，则 $P (μ - σ < x \leq μ + σ) = 0.6826$ ， $P (μ - 2 σ < x \leq μ + 2 σ) = 0.9544$ ， $P (μ - 3 σ < x \leq μ + 3 σ) = 0.9974$ ）．

查看试题解析