浙教版备考2021年中考数学一轮复习专题26——梯形、中点四边形
试卷更新日期:2021-02-14 类型:一轮复习
一、单选题
-
1. 梯形的下底比上底多2cm,高是5cm,面积是40cm2 , 则上底长为( )A、9cm B、7cm C、5cm D、3cm2. 四边形ABCD各角之比∠A:∠B:∠C:∠D=1:2:3:4,则这个四边形为( )A、平行四边形 B、菱形 C、等腰梯形 D、梯形3. 如图所示(单位:分米),等腰梯形中阴影部分的面积是( )
 A、24 B、30 C、54 D、604. 在梯形 中, // ,那么下列条件中,不能判断它是等腰梯形的是( )A、 B、 C、 D、5. 顺次连接矩形各边中点得到的四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形6. 下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )A、
A、24 B、30 C、54 D、604. 在梯形 中, // ,那么下列条件中,不能判断它是等腰梯形的是( )A、 B、 C、 D、5. 顺次连接矩形各边中点得到的四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形6. 下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是( )
7. 如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是( ) A、PD>PC B、PD=PC C、PD<PC D、无法判断8. 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ,CD=3 ,点P在四边形ABCD的边上,若 的面积是12,则点P的个数为( )
A、PD>PC B、PD=PC C、PD<PC D、无法判断8. 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ,CD=3 ,点P在四边形ABCD的边上,若 的面积是12,则点P的个数为( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
9. 如图,在直角梯形ABCD中,AB⊥BC,AD∥BC,EF为中位线,若AB=2b,EF=a,则阴影部分的面积.
 10. 如图所示,在梯形ABCD中,AD∥BC,AB=DC,BD⊥DC,且BD平分∠ABC,若梯形的周长为20cm,梯形的中位线的长为 cm.
10. 如图所示,在梯形ABCD中,AD∥BC,AB=DC,BD⊥DC,且BD平分∠ABC,若梯形的周长为20cm,梯形的中位线的长为 cm. 11. 有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2 米,那么此拦水坝的坡角为度.12. 如果一个等腰梯形中位线的长是5cm,腰长是4cm,那么它的周长是cm.13. 如图, 是 的中位线, cm, cm,则梯形 的周长为cm.
11. 有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2 米,那么此拦水坝的坡角为度.12. 如果一个等腰梯形中位线的长是5cm,腰长是4cm,那么它的周长是cm.13. 如图, 是 的中位线, cm, cm,则梯形 的周长为cm. 14. 如图,A、C在双曲线y=﹣ 上,B、D在双曲线y= 上,AB∥x轴,BC∥y轴,AD∥y轴,则四边形ABCD的面积是.
14. 如图,A、C在双曲线y=﹣ 上,B、D在双曲线y= 上,AB∥x轴,BC∥y轴,AD∥y轴,则四边形ABCD的面积是. 15. 如图,以 为直径的 的圆心 到直线 的距离 , 的半径 ,直线 不垂直于直线 ,过点 、 分别作直线 的垂线,垂足分别为点 、 ,则四边形 的面积的最大值为.
15. 如图,以 为直径的 的圆心 到直线 的距离 , 的半径 ,直线 不垂直于直线 ,过点 、 分别作直线 的垂线,垂足分别为点 、 ,则四边形 的面积的最大值为. 16. 如图,在四边形ABCD中,对角线 AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH 的面积为 .
16. 如图,在四边形ABCD中,对角线 AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH 的面积为 . 17. 如图,10个边长为1的正方形摆放在平面直角坐标系中,经过A(1,0)点的一条直线l将这10个正方形分成面积相等的两部分,则该直线的解析式为.
17. 如图,10个边长为1的正方形摆放在平面直角坐标系中,经过A(1,0)点的一条直线l将这10个正方形分成面积相等的两部分,则该直线的解析式为.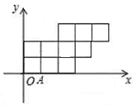 18. 如图,直线 轴于点 ,直线 轴于点 ,直线 轴于点 ,…,直线 轴于点 (其中 为正整数).函数 的图象与直线 , , ,…, 分别交于点 , , ,…, ;函数 的图象与直线 , , ,…, 分别交于点 , , ,…, ,如果 的面积记作 ,四边形 的面积记作 ,四边形 的面积记作 ,…,四边形 的面积记作 ,那么 .
18. 如图,直线 轴于点 ,直线 轴于点 ,直线 轴于点 ,…,直线 轴于点 (其中 为正整数).函数 的图象与直线 , , ,…, 分别交于点 , , ,…, ;函数 的图象与直线 , , ,…, 分别交于点 , , ,…, ,如果 的面积记作 ,四边形 的面积记作 ,四边形 的面积记作 ,…,四边形 的面积记作 ,那么 .
三、综合题
-
19. 如图:等腰梯形ABCD中,AD∥BC,AB=DC,AD=3,AB=4,∠B=60°
求梯形的面积.
 20. 如图,△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线,则四边形EBCD是等腰梯形吗?为什么?
20. 如图,△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线,则四边形EBCD是等腰梯形吗?为什么? 21. 如图,在梯形ABCD中,AD∥BC , BC=12,AB=DC=8.∠B=60°.
21. 如图,在梯形ABCD中,AD∥BC , BC=12,AB=DC=8.∠B=60°.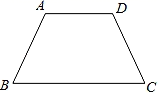 (1)、求梯形的中位线长.(2)、求梯形的面积.22. 如图,四边形ABCD中, BAD= BCD=90°,E为对角线BD的中点,连接AE、CE.
(1)、求梯形的中位线长.(2)、求梯形的面积.22. 如图,四边形ABCD中, BAD= BCD=90°,E为对角线BD的中点,连接AE、CE. (1)、求证:AE=CE;(2)、若AC=8,BD=10,求△ACE的面积.
(1)、求证:AE=CE;(2)、若AC=8,BD=10,求△ACE的面积.

