浙教版备考2021年中考数学一轮复习专题25——正方形
试卷更新日期:2021-02-10 类型:一轮复习
一、单选题
-
1. 顺次连接四边形各边中点所构成的四边形是正方形,则原四边形可能是( )A、平行四边形 B、矩形 C、菱形 D、正方形2. 已知在四边形 中, ,下列可以判定四边形是正方形的是( )A、 B、 C、 D、3. 下列命题是假命题的是( )A、对角线互相垂直且相等的平行四边形是正方形. B、对角线互相垂直的矩形是正方形. C、对角线相等的菱形是正方形. D、对角线互相垂直平分的四边形是正方形.4. 如图,把一个长方形的纸片对折两次,然后剪下一个角,要得到一个正方形,剪口与折痕所成锐角的大小为( )
 A、 B、 C、 D、5. 如图,四边形ABCD是正方形,直线L1、L2、L3 , 若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )
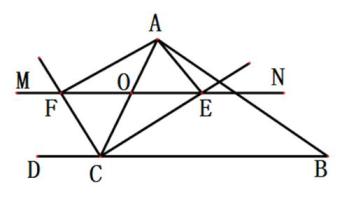
A、 B、 C、 D、5. 如图,四边形ABCD是正方形,直线L1、L2、L3 , 若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )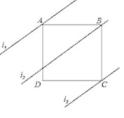 A、70 B、74 C、144 D、1486. 如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( )
A、70 B、74 C、144 D、1486. 如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( ) A、22.5° B、30° C、45° D、67.5°7. 如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
A、22.5° B、30° C、45° D、67.5°7. 如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.

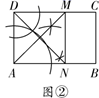
对于以上两种作法,可以做出的判定是( )
A、甲正确,乙不正确 B、甲、乙正确 C、乙正确,甲不正确 D、甲、乙均不正确8. 如图,是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( ). A、4或6 B、3或5 C、1或7 D、3或69.
A、4或6 B、3或5 C、1或7 D、3或69.如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
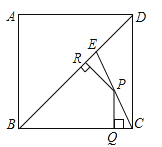 A、2 B、2 C、2 D、10. 如图,在正方形 中,点 是 的中点,点 是 的中点, 与 相交于点 ,设 .得到以下结论:① ;② ;③ 则上述结论正确的是( )
A、2 B、2 C、2 D、10. 如图,在正方形 中,点 是 的中点,点 是 的中点, 与 相交于点 ,设 .得到以下结论:① ;② ;③ 则上述结论正确的是( )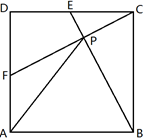 A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 若一个正方形的面积为a2+a+ ,则此正方形的周长为.12. 如图,正方形ABCD的边长为4厘米,则图中阴影部分的面积为.
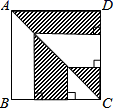 13. 如图,两个正方形Ⅰ,Ⅱ和两个矩形Ⅲ,Ⅳ拼成一个大正方形,已知正方形Ⅰ,Ⅱ的面积分别为10和3,那么大正方形的面积是.
13. 如图,两个正方形Ⅰ,Ⅱ和两个矩形Ⅲ,Ⅳ拼成一个大正方形,已知正方形Ⅰ,Ⅱ的面积分别为10和3,那么大正方形的面积是.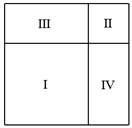 14. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为
14. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为 15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则 的值为 .
15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则 的值为 . 16. 如图,三个边长均为2的正方形重叠在一起,O1 , O2是其中两个正方形的对角线交点,若把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为 .
16. 如图,三个边长均为2的正方形重叠在一起,O1 , O2是其中两个正方形的对角线交点,若把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为 . 17. 如图,在△ABC中,分别以AB,AC为边向外作正方形ABED,ACGF。若点E,A,G在同一直线上,EG=8 ,BC=7,则△ABC的面积为。
17. 如图,在△ABC中,分别以AB,AC为边向外作正方形ABED,ACGF。若点E,A,G在同一直线上,EG=8 ,BC=7,则△ABC的面积为。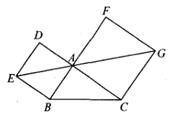 18. 如图,抛物线 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC , 延长CB交抛物线于点D , 再以BD为边向上作正方形BDEF . 则E的坐标是 .
18. 如图,抛物线 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC , 延长CB交抛物线于点D , 再以BD为边向上作正方形BDEF . 则E的坐标是 .
三、综合题
-
19. 如图,四边形 是正方形,对角线 、 相交于点F, , .求证:四边形 是正方形.
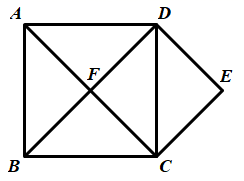 20. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.
20. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.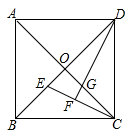 21. 如图,点O为正方形ABCD的对角线交点,将线段OE绕点O逆时针方向旋转 ,点E的对应点为点F,连接EF,AE,BF.
21. 如图,点O为正方形ABCD的对角线交点,将线段OE绕点O逆时针方向旋转 ,点E的对应点为点F,连接EF,AE,BF. (1)、请依题意补全图形;
(1)、请依题意补全图形;
(2)、根据补全的图形,猜想并证明直线AE与BF的位置关系.
22. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1 , 点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 S2 , 且S1=S2. (1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.
(1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.