浙教版备考2021年中考数学一轮复习专题24——菱形
试卷更新日期：2021-02-10 类型：一轮复习
一、单选题
-
1. 菱形的两条对角线分别为8和6，则菱形的周长和面积分别是
A、20，48 B、14，48 C、24，20 D、20，242. 菱形 的边长是 ，一条对角线 的长是 ，则此菱形的面积为（ ）A、 B、 C、 D、3. 已知菱形 中，对角线 与 交于点O， ， ，则该菱形的周长是（ ）
A、13 B、52 C、120 D、2404. 下面性质中，菱形不一定具备的是（ ）A、四条边都相等 B、每一条对角线平分一组对角 C、邻角互补 D、对角线相等5. 菱形的一条对角线与它的边相等，则它的锐角等于（ ）A、30° B、45° C、60° D、75°6. 如图，某同学作线段AB的垂直平分线：分别以点A和点B为圆心，大于 AB的长为半径画弧，两弧相交于点C，D，则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是（ ）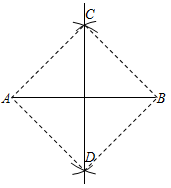
A、菱形 B、平行四边形 C、矩形 D、一般的四边形7. 如图，在△ABC中中，AD平分∠BAC，DE AC交AB于点E，DF AB交AC于点F，若AF＝8，则四边形AEDF的周长是（ ）
A、24 B、28 C、32 D、368. 如图，菱形ABCD的对角线AC、BD交于点O ， AC=8，BD=6，DE⊥AB于点E ， 则DE的长为（ ）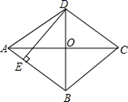
A、4.8 B、5 C、9.6 D、109. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，OH＝4，则菱形ABCD的面积为（ ）
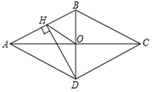A、72 B、24 C、48 D、9610. 如图，已知在平面直角坐标系中，四边形ABCD是菱形，其中B点坐标是(8，2)，D点坐标是(0，2)，点A在x轴上，则菱形ABCD的周长是（ ）
A、2 B、8 C、8 D、12二、填空题
-
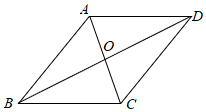
11. 如图，在菱形ABCD中，对角线AC，BD交于点O，其中OA＝1，OB＝2，则菱形ABCD的面积为.
12. 如图，菱形 的周长为 ，对角线 与 相交于点 ， ， ，垂足为 ，则 .
13. 已知菱形的边长为4，一个内角为60°，则菱形较短的对角线长为 ．14. 如图，在菱形ABCD中，过点B作BE⊥AD ， BF⊥CD ， 垂足分别为点E ， F ， 延长BD至点G ， 使得DG＝BD ， 连结EG ， FG ． 若AE＝DE ， AB＝2，则EG＝ ．
15. 如图，在菱形ABCD中，过点A作AH⊥BC，分别交BD，BC于点E，H，F为ED的中点， ，则∠C的度数为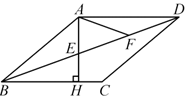
16. 如图，在边长为1的菱形 ABCD中，∠ABC＝120°.连接对角线AC，以AC为边作第二个菱形ACEF，使∠ACE＝120°.连接AE，再以AE为边作第三个菱形AEGH，使 ∠AEG＝120°，…，按此规律所作的第n个菱形的边长是 ．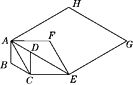
三、综合题
-
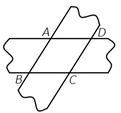
17. 如图，两张等宽的纸条交叉重叠在一起，重叠的部分ABCD是菱形吗？为什么？
18. 如图，在 中，以点B为圆心， 长为半径画弧，交 于点E，在 上截取 ，连接 .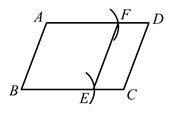
(1)、求证：四边形 是菱形；(2)、请用无刻度的直尺在 内找一点P，使 （标出点P的位置，保留作图痕迹，不写作法）19. 如图，四边形ABCD是菱形，BE⊥AD、BF⊥CD，垂足分别为E、F.
(1)、求证：BE＝BF；(2)、当菱形ABCD的对角线AC＝8，BD＝6时，求BE的长.20. 如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC、BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E．连接OE．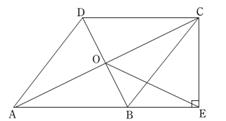
(1)、求证：四边形ABCD是菱形；(2)、若AB＝ ．OE＝2，求线段CE的长．
