浙教版备考2021年中考数学一轮复习专题22——多边形和平行四边形
试卷更新日期:2021-02-08 类型:一轮复习
一、单选题
-
1. 五边形的对角线共有( )A、3条 B、4条 C、5条 D、6条2. 在下列正多边形瓷砖中,若仅用一种正多边形瓷砖铺地面,则不能将地面密铺的是( )A、正三角形 B、正四边形 C、正六边形 D、正八边形3. 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )
 A、21 B、18 C、15 D、134. 已知三角形的三条中位线的长分别是 ,则这个三角形的周长为( )A、6.5 B、13 C、24 D、265. 在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的面积之比为( )A、 B、 C、 D、6. 如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是( )
A、21 B、18 C、15 D、134. 已知三角形的三条中位线的长分别是 ,则这个三角形的周长为( )A、6.5 B、13 C、24 D、265. 在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的面积之比为( )A、 B、 C、 D、6. 如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是( )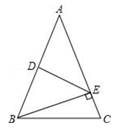 A、6 B、 C、 D、107. 如图,抛物线y=﹣2x2+2与x轴交于点A、B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1 , 将C1向右平移得到C2 , C2与x轴交于点B、D,C2的顶点为F,连结EF.则图中阴影部分图形的面积为( )
A、6 B、 C、 D、107. 如图,抛物线y=﹣2x2+2与x轴交于点A、B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1 , 将C1向右平移得到C2 , C2与x轴交于点B、D,C2的顶点为F,连结EF.则图中阴影部分图形的面积为( )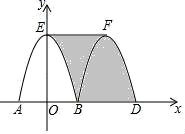 A、1 B、2 C、3 D、48. 如图,四张大小不一的正方形分别放置于矩形的四个角落.在矩形ABCD的周长已知的情况下,只有知道下列哪个正方形的边长,就可以求得阴影部分的周长( )
A、1 B、2 C、3 D、48. 如图,四张大小不一的正方形分别放置于矩形的四个角落.在矩形ABCD的周长已知的情况下,只有知道下列哪个正方形的边长,就可以求得阴影部分的周长( )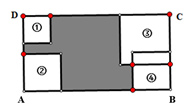 A、① B、② C、③ D、④9. 如图,多边形 中, , ,则 的值为( )
A、① B、② C、③ D、④9. 如图,多边形 中, , ,则 的值为( )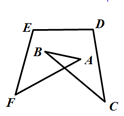 A、84° B、80° C、72° D、60°10. 如图,菱形ABCD的对角线相交于点O , AC=12,BD=16,点P为边BC上一点,且点P不与点B、C重合.过点P作PE⊥AC于点E , PF⊥BD于点F , 连结EF , 则EF的最小值为( )
A、84° B、80° C、72° D、60°10. 如图,菱形ABCD的对角线相交于点O , AC=12,BD=16,点P为边BC上一点,且点P不与点B、C重合.过点P作PE⊥AC于点E , PF⊥BD于点F , 连结EF , 则EF的最小值为( )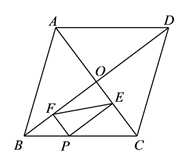 A、4 B、4.8 C、5 D、6
A、4 B、4.8 C、5 D、6二、填空题
-
11. 从某多边形的一个顶点出发,连接其余各顶点,把这个多边形分成 个三角形,则这个多边形是.12. 如图,小亮从点A出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°…… 照这样走下去,他第一次回到出发地点A时,共走了米.
 13. 一个平行四边形的面积为 平方米,一条边长为 米,则这条边上的高为米.14. 如图,在平行四边形 中, 平分 , , ,则 的周长是.
13. 一个平行四边形的面积为 平方米,一条边长为 米,则这条边上的高为米.14. 如图,在平行四边形 中, 平分 , , ,则 的周长是.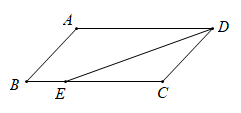 15. 如图,点A是反比例函数y= 图像上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为4,则k= 。
15. 如图,点A是反比例函数y= 图像上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为4,则k= 。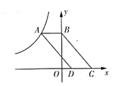 16. 如图,在 中,已知 依次连接 的三边中点, 得 ,再依次连接 的三边中点得 ,···,则 的周长为 .
16. 如图,在 中,已知 依次连接 的三边中点, 得 ,再依次连接 的三边中点得 ,···,则 的周长为 .
三、综合题
-
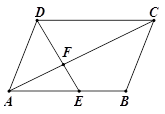
17. 如图,在平行四边形 中, .
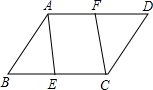
求证: .
18. 如图,在正方形ABCD中,点E是对角线BD上一点,连接AE,将DE绕D点逆时针方向旋转90°到DF,连接BF,交DC于点G,若DG=3,CG=2,则线段AE的长为.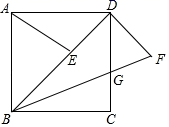 19. 在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°.(1)、求这个多边形的边数.(2)、求这个多边形的内角和及对角线的条数.20. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
19. 在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°.(1)、求这个多边形的边数.(2)、求这个多边形的内角和及对角线的条数.20. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).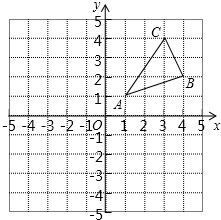 (1)、请画出△ABC关于原点对称的△A1B1C1;(2)、四边形CBC1B1为四边形;(3)、点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
(1)、请画出△ABC关于原点对称的△A1B1C1;(2)、四边形CBC1B1为四边形;(3)、点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.