浙教版备考2021年中考数学一轮复习专题19——角平分线与线段垂直平分线

试卷更新日期：2021-02-08 类型：一轮复习

进入出卷网下载

一、单选题

1. 如图，直线AC和直线BD相交于点O，OE平分∠BOC.若∠1+∠2＝80°，则∠3的度数为（）

A、40° B、50° C、60° D、70°

查看试题解析
2. 到三角形的三个顶点距离相等的点是（　　）

A、三条角平分线的交点 B、三条边的垂直平分线的交点 C、三条高的交点 D、三条中线的交点

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ C A B$ 的角平分线， $D E ⊥ A B$ 于点E，若 $B C = 6 cm$ ， $B D = 4 cm$ .则 $D E$ 的长是（）

A、 $5 cm$ B、 $4 cm$ C、 $3 cm$ D、 $2 cm$

查看试题解析
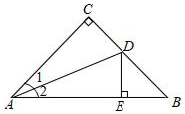4. 如图，以△ABD的顶点B为圆心，以BD为半径作弧交边AD于点E，分别以点D、点E为圆心，BD长为半径作弧，两弧相交于不同于点B的另一点F，再过点B和点F作直线BF，则作出的直线是（）

A、线段AD的垂线但不一定平分线段AD B、线段AD的垂直平分线 C、∠ABD的平分线 D、△ABD的中线

查看试题解析
5. 如图，在△ABC中，∠C＝90°，D，E是AC上两点，且AE＝DE，BD平分∠EBC，那么下列说法中不正确的是（）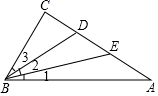

A、BE是△ABD的中线 B、BD是△BCE的角平分线 C、∠1＝∠2＝∠3 D、BC是△ABE的高

查看试题解析
6. 作 $∠ A O B$ 的平分线时，以O为圆心，某一长度为半径作弧，与OA，OB分别相交于C，D，然后分别以C，D为圆心，适当的长度为半径作弧使两弧在 $∠ A O B$ 的内部相交于一点，则这个适当的长度（）

A、大于 $\frac{1}{2} C D$ B、等于 $\frac{1}{2} C D$ C、小于 $\frac{1}{2} C D$ D、以上都不对

查看试题解析
7. 如图，在△ABC中，AB的垂直平分线交AB于点E，交BC于点D，△ADC的周长为10，且BC-AC=2，则BC的长为（）

A、 $4$ B、 $6$ C、 $8$ D、 $10$

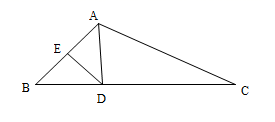查看试题解析
8. 如图，在 $△ A B C$ 中，A B=2020，AC=2018，AD为中线，则 $△ A B D$ 与 $△ A C D$ 的周长之差为（）

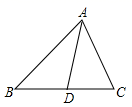A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 如图，点P到∠AOB两边的距离相等，若∠POB＝30°，则∠AOB＝.

查看试题解析
10. 如图，在 $△ A B C$ 中，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 长为半径画弧，两弧相交于点M，N，作直线 $M N$ 分别交 $B C$ ， $A C$ 于点D，E.若 $A E = 3$ ， $△ A B D$ 的周长为13，则 $△ A B C$ 的周长为.

查看试题解析
11. 如图OA⊥OB，∠BOC=30°，OD平分∠AOC，则∠BOD的度数是度。

查看试题解析
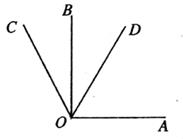12. 如图，∠A=90°，∠ABC的角平分线交AC于E，AE=3，则E到BC的距离为．

查看试题解析
13. 有三条两两相交的公路，要建一个加油站，使它到三条公路的距离相等，那么加油站可建的地点有个.

查看试题解析
14. 如图，在菱形 $A B C D$ 中， $∠ A = 30 °$ ，取大于 $\frac{1}{2} A B$ 的长为半径，分别以点 $A$ ， $B$ 为圆心作弧相交于两点，过此两点的直线交 $A D$ 边于点 $E$ （作图痕迹如图所示），连接 $B E$ ， $B D$ ，则 $∠ E B D$ 的度数为．

查看试题解析

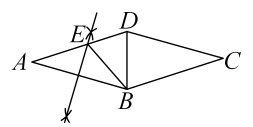
三、综合题

15. 对下面每个三角形，过顶点A画出中线，角平分线和高.

查看试题解析
16. 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在何处.（不写作法，保留作图痕迹）

查看试题解析
17. 尺规作图：如图，在 $Δ A B C$ 中

(1)、作 $Δ A B C$ 的角平分线 $A M$ ；

(2)、作 $A C$ 边的中线 $B N$

查看试题解析
18. 在锐角三角形ABC中，D是BC的中点，DE^AB于E，DF^AC于F，且BE=CF，求证：AD是∠BAC的平分线；

查看试题解析
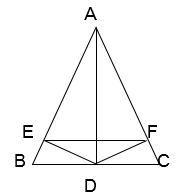19. 如图，在Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，连接CD，交BE于点F.
求证：BE垂直平分CD.

查看试题解析
20. 在 $△ A B C$ 中， $A B$ 的垂直平分线 $l_{1}$ 交 $B C$ 于点 $D$ ， $A C$ 的垂直平分线 $l_{2}$ 交 $B C$ 于点 $E$ ， $l_{1}$ 与 $l_{2}$ 相交于点 $O$ ， $△ A D E$ 的周长为6．

(1)、 $A D$ 与 $B D$ 的数量关系为．

(2)、求 $B C$ 的长．

(3)、分别连接 $O A$ ， $O B$ ， $O C$ ，若 $△ O B C$ 的周长为16，求 $O A$ 的长．

查看试题解析
21. 如图，点A、O、B三点共线，OC是过点O的任意一条射线，

(1)、若OM、ON分别是 $∠ A O C$ 、 $∠ B O C$ 的角平分线，求 $∠ M O N$ .

(2)、 $∴ ∠ M O N = ∠ C O M + ∠ C O N = \frac{1}{2} ∠ A O C + \frac{1}{2} ∠ C O B = \frac{1}{2} \times (∠ A O C + ∠ C O B) = 90^{0} .$ 若OM、ON分别是 $∠ A O C$ 、 $∠ B O C$ 的一条三等分线， $∠ A O M = \frac{1}{3} ∠ A O C$ ， $∠ B O N = \frac{1}{3} ∠ B O C$ ，求 $∠ M O N$ .

(3)、 $∴ ∠ M O N = ∠ C O M + ∠ C O N = \frac{2}{3} ∠ A O C + \frac{2}{3} ∠ C O B = \frac{2}{3} \times (∠ A O C + ∠ C O B) = \frac{2}{3} \times 180^{°} = 120^{°} .$ 根据（1）、（2）的结果，猜想，若OM、ON分别是 $∠ A O C$ 、 $∠ B O C$ 的一条n等分线， $∠ A O M = \frac{1}{n} ∠ A O C$ ， $∠ B O N = \frac{1}{n} ∠ B O C$ ，则 $∠ M O N =$ .

查看试题解析