浙教版备考2021年中考数学一轮复习专题17——相交线与平行线
试卷更新日期：2021-02-07 类型：一轮复习
一、单选题
-
1. 如图，直线 相交于点 ，已知 ，则 的度数为（ ）
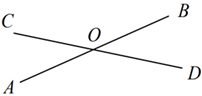A、 B、 C、 D、2. 如图，直线 ， 相交，若 ，则 （ ）
A、45° B、55° C、145° D、155°3. 如图，图中共有12个角，其中内错角有（ ）对
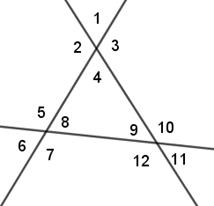A、6 B、12 C、4 D、84. ， ， 是同一平面内的三条直线，下列说法错误的是（ ）A、如果 ， ，那么 B、如果 ， ，那么 C、如果 ， ，那么 D、如果 ， ，那么5. 如图， ∠1与∠2的关系是（ ）
A、对顶角 B、同位角 C、内错角 D、同旁内角6. 已知点Ｍ(9，-5)、N(-3，-5)，则直线MN与x轴、y轴的位置关系分别为（ ）A、相交、相交 B、平行、平行 C、垂直相交、平行 D、平行、垂直相交7. 在广场上练习驾驶汽车，两次拐弯后，驶方向与原来相同，这两次弯的角度可能是（ ）A、第一次左拐30°，第二次右拐30° B、第一次右拐50°，第二次左拐130° C、第一次右拐50°，第二次右拐130° D、第一次左拐50°，第二次左拐120°8. 两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，…那么六条直线最多有（ ）A、21个交点 B、18个交点 C、15个交点 D、10个交点9. 如图，点P是 中斜边AC（不与A，C重合）上一动点，分别作PM⊥AB于点M，作PN⊥BC于点N，点O是MN的中点，若AB=6；BC=8，当点P在AC上运动时，则BO的最小值是（ ）
A、1.5 B、2 C、2.4 D、2.5二、填空题
-
10. 如图，已知ON⊥l，OM⊥l，所以OM与ON重合，其理由是.
11. 如图，同旁内角有对．
12. 如图所示，C岛在A岛的北偏东50°方向，C岛在B岛的北偏西40°方向，则从C岛看A、B两岛的视角∠ACB等于.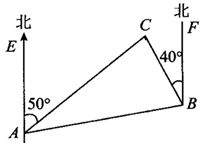
13. 在同一平面内，三条互不重合的直线 a 、 b 、 ，若 a ⊥ b ， a ⊥ ，则.
14. 如图，已知 ， ， ，且 ， 垂足分别为E，F．则AD与BC间的距离是 ．
15. 已知一次函数 ，当 变化时，原点到一次函数 的图象的最大距离为 ．16. 一副直角三角尺如图①叠放，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，要求两块三角尺的一组边互相平行.如图②，当∠BAD=15°时，有一组边BC∥DE，请再写出两个符合要求的∠BAD（0°＜∠BAD＜180°）的度数.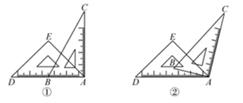
三、综合题
-
17. 如图，在△ABC中，画出BC边上的高AD和中线AE
18. 如图，已知∠ABC ， 求作：▱ABCD（要求：①尺规作图，保留作图痕迹，不写作法；②用两种方法作图）
19. 如图，直线 分别交 和 于点 、 ，点 在 上， ，且 .求证： ．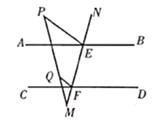
20. 如图，C为线段 外一点．
(1)、求作四边形 ，使得 ，且 ；（要求：尺规作图，不写作法，保留作图痕迹）(2)、在（1）的四边形 中， ， 相交于点P， ， 的中点分别为 ，求证： 三点在同一条直线上．21. 如图，已知△ABC中，AD⊥BC于点D，E为AB边上任意一点，EF⊥BC于点F，∠1=∠2.求证：DG∥AB.请把证明的过程填写完整.
证明：∵AD⊥BC，EF⊥BC（ ），
∴∠EFB=∠ADB=90°（垂直的定义）
∴EF∥ ▲ （ ）
∴∠1= ▲ （ ）
又∵∠1=∠2（已知）
∴ ▲ （ ）
∴DG∥AB（ ）
22. 如图，∠1+∠2＝180°，∠B＝∠3.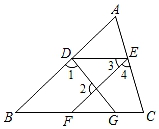
(1)、判断DE与BC的位置关系，并说明理由；(2)、若∠C＝70°，∠2＝80°，∠4＝65°，求∠FGD的度数.23. 我们把能平分四边形面积的直线称为“好线”．利用下面的作图，可以得到四边形的“好线”：如图1四边形ABCD中，取对角线BD的中点O，连接OA，OC，显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”．
(1)、如图1，试说明直线AE是“好线”的理由；(2)、如图2，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，并说明理由；(3)、如图3，五边形ABCDE是一块土地的示意图，经过多年开垦荒地，现已变成如图3所示的形状，但原块土地与开垦荒地的分界小路（折线CDE）还保留着，现在请你过E点修一条直路．要求直路左边的土地面积与原来一样多（只需对作图适当说明无需说明理由）