青海省海东市2020年九年级下学期数学中考三模试卷

试卷更新日期：2021-02-03 类型：中考模拟

进入出卷网下载

一、填空题

1. $- 3$ 的倒数是；64的平方根是.

查看试题解析
2. 不等式 $2 x + 15 > - x$ 的解集是；分解因式： $2 x^{2} - 2 =$ .

查看试题解析
3. 蜜蜂在飞行过程中，翅膀每分钟振动约14000次，数据14000用科学记数法表示为.

查看试题解析
4. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + a - 1 = 0$ 有实数根，则 $a$ 的取值范围为.

查看试题解析
5. 如图，两条平行直线 $A M$ ， $B N$ 分别交 $∠ B S D$ 的两边于点 $A ， C ， B ， D$ ，若 $S A = 2$ ， $A B = 1.5$ ， $S C = 1.6$ ，则 $S D =$ .

查看试题解析
6. 如图，将 $Δ O A B$ 绕点 $O$ 逆时针旋转 $20 °$ 得到 $Δ O C D$ ，若点 $B$ 在 $C D$ 上，则 $∠ O B A =$ .

查看试题解析
7. 分式方程 $\frac{x + 2}{x - 1} + 1 = 0$ 的解为．

查看试题解析
8. 如图， $P$ 是反比例函数位于第四象限图象上一点，过点 $P$ 作 $P A ⊥ x$ 轴于点 $A$ ， $P B ⊥ y$ 轴于点 $B$ ，若四边形 $A O B P$ 的面积为4，则该反比例函数的解析式为.

查看试题解析
9. 现在有一面7尺厚的墙，大小两只老鼠分别从两面相对着打洞，第一天两只老鼠都打相同距离的洞，从第二天开始，大老鼠每天打洞的距离是前一天的2倍，小老鼠每天打洞的距离是前一天的一半，第三天结束洞刚好被打通，小老鼠第一天打洞的距离为尺.

查看试题解析
10. 根据如图所示的程序计算函数 $y$ 的值，若输入 $x$ 的值是8，则输出 $y$ 的值是 $- 3$ ；若输入 $x$ 的值是 $- 8$ ，则输出 $y$ 的值是.

查看试题解析
11. 如图，已知正方形 $A B C D$ 的边长为4，对角线 $A C$ ， $B D$ 交于点 $E$ ，分别以 $A B$ ， $C D$ 为直径作半圆，则图中阴影部分的面积为.

查看试题解析
12. 如图所示的是一组有规律的图案，图案（1）是由4个组成的，图案（2）是由7个组成的，图案（3）是由10个组成的，以此类推，图案（5）是由个组成的，图案（ $n$ ）是由个组成的.（用含 $n$ 的代数式表示）

查看试题解析

二、单选题

13. 如图所示的是由一些相同的小立方块搭成的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
14. 将一副直角三角尺按如图所示的方式摆放在一起，其中 $∠ B = ∠ F = 90 °$ ， $∠ A = 45 °$ ， $∠ E = 60 °$ ，点 $C$ 在边 $D F$ 上， $A C$ ， $B C$ 分别交 $D E$ 于点 $G$ ， $H$ .若 $B C ∥ E F$ ，则 $∠ A G D$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
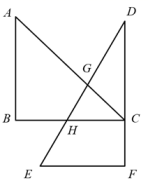15. 某工厂为了解工人加工某工件的情况，随机抽取了部分工人一天加工该工件的个数进行了统计，统计数据如表所示，则被抽取的工人一天加工该工件的中位数和众数分别是（）

一天加工该工件的个数（个）

70

80

90

100

110

工人人数

4

11

10

8

7

A、90，80 B、90，90 C、95，90 D、95，80

查看试题解析
16. 佳佳制作了一个圆锥形的紫绸帽子，经测量，圆锥的母线长为 $40 c m$ ，所用紫绸面积为 $360 π c m^{2}$ （不计接头损耗），则圆锥的底面直径为（）

A、 $6 c m$ B、 $9 c m$ C、 $18 c m$ D、 $36 c m$

查看试题解析
17. 如图所示的是一个可以自由转动的转盘，转盘停止后，指针落在阴影区域的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{7}{12}$

查看试题解析
18. 如图， $Δ A B C$ 与 $Δ D E F$ 位似，其位似中心为点 $O$ ，且 $O D = A D$ ，则 $Δ A B C$ 与 $Δ D E F$ 的位似比是（）

A、 $2 ： 1$ B、 $4 ： 1$ C、 $\sqrt{2} ： 1$ D、 $2 ： \sqrt{3}$

查看试题解析
19. 如图，在平面直角坐标系中，四边形 $O A B C$ 是矩形， $O A = 6$ ，将 $Δ A B C$ 沿直线 $A C$ 翻折，使点 $B$ 落在点 $D$ 处， $A D$ 交 $x$ 轴于点 $E$ ，若 $∠ B A C = 30 °$ ，则点 $D$ 的坐标为（）

A、 $(3 \sqrt{3} ， - 2)$ B、 $(3 \sqrt{3} ， - 3)$ C、 $(\sqrt{3} ， - 3)$ D、 $(3 ， - 3 \sqrt{3})$

查看试题解析
20. 若实数 $a ， b ， c$ 满足 $a + b + c = 0$ ，且 $a > b > c$ ，则关于 $x$ 的一次函数 $y = - c x - a$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析

三、解答题

21. 计算： $\sqrt[3]{\frac{27}{8}} - \sqrt{2} \cos 45^{°} + {(- 2)}^{0} - {(\frac{1}{2})}^{- 1}$ .

查看试题解析
22. 先化简，再求值： $\frac{x^{2} + 2 x + 1}{x^{2} - 4} \div (\frac{1}{x + 2} - 1)$ ，其中 $x = 2 + \sqrt{3}$ .

查看试题解析
23. 如图，四边形 $A E C F$ 是菱形， $B ， D$ 两点分别在 $F E$ ， $E F$ 的延长线上，且 $B E = D F$ ，连接 $A B$ ， $B C$ ， $C D$ ， $A D$ .

(1)、求证： $Δ A E B ≌ Δ C F D$ .

(2)、求证：四边形 $A B C D$ 是菱形.

查看试题解析
24. 如图，在瞭望塔 $A B$ 前有一段坡比为 $1 ： \sqrt{2}$ 的斜坡 $B C$ ，经测量 $B C = 8 \sqrt{3}$ 米，在海岸上取点 $D$ ，使 $C D = 45$ 米，在点 $D$ 测得瞭望塔顶端 $A$ 的仰角为 $40 °$ ，求瞭望塔 $A B$ 的高度约为多少米.（结果精确到0.1米，参考数据： $\sin 40 ° \approx 0.64$ ， $\cos 40 ° \approx 0.77$ ， $\tan 40 ° \approx 0.84$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
25. 如图，在等腰三角形 $A B D$ 中， $A B = A D$ ，点 $C$ 为 $B D$ 上一点，以 $B C$ 为直径作 $⊙ O$ ，且点 $A$ 恰好在 $⊙ O$ 上，连接 $A C$ .

(1)、若 $A C = C D$ ，求证： $A D$ 是 $⊙ O$ 的切线.

(2)、在（1）的条件下，若 $C D = 1$ ，求 $⊙ O$ 的直径.

查看试题解析
26. 为鼓励学生阅读，某校开展了网上阅读室活动，校教务处为了解学生的阅读情况，随机抽查了部分学生最近一周参加网上阅读室的天数，并用得到的数据绘制了如下两幅统计图.
请根据图中提供的信息，回答下列问题：

(1)、 $a =$ （百分比），本次调查的参加网上阅读室的天数的中位数为.

(2)、请补全条形统计图.

(3)、如果该校有3000名学生，请估算全校有多少名学生参加网上阅读室的天数不少于4天.

(4)、在某班被调查的学生中，参加网上阅读室的天数不少于4天的有2名女同学，3名男同学.现要从中随机抽取2名同学代表班级参加阅读心得分享会，请用列表法或画树状图法求所抽取的2名同学恰好是一男一女的概率.

查看试题解析
27. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与坐标轴的交点为 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ， $C (0 ， - 3)$ ，抛物线的顶点为 $D$ .

(1)、求抛物线的解析式.

(2)、若 $E$ 为第二象限内一点，且四边形 $A C B E$ 为平行四边形，求直线 $C E$ 的解析式.

(3)、 $P$ 为抛物线上一动点，当 $Δ P A B$ 的面积是 $Δ A B D$ 的面积的3倍时，求点 $P$ 的坐标.

查看试题解析
28. 请认真阅读下面的数学探究，并完成所提出的问题.

(1)、探究1：如图1，在边长为 $a$ 的等边三角形 $A B C$ 中， $P$ 是 $B C$ 边上任意一点，连接 $A P$ ，将 $Δ A P C$ 绕点 $A$ 按顺时针方向旋转至 $Δ A B Q$ 处，连接 $P Q$ ，求 $Δ A P Q$ 面积的最小值.

(2)、探究2：如图2，若 $Δ A B C$ 是腰长为 $a$ 的等腰直角三角形， $∠ B A C = 90 °$ ，（1）中的其他条件不变，请求出此时 $Δ A P Q$ 面积的最小值.

(3)、探究3：如图3，在 $Δ A B C$ 中， $A C = a$ ， $∠ C = 30 °$ ， $∠ A B C = 90 °$ ， $P$ 是 $B C$ 边上任意一点，连接 $A P$ ，将 $Δ A P C$ 绕点 $A$ 按顺时针方向旋转至 $Δ A Q D$ 处， $A$ 、 $B$ 、 $D$ 三点共线，连接 $P Q$ ，求 $Δ A P Q$ 的面积的最小值.

查看试题解析

一天加工该工件的个数（个）	70	80	90	100	110
工人人数	4	11	10	8	7