海南省琼海市2020届九年级下学期数学中考一模试卷
试卷更新日期:2021-02-03 类型:中考模拟
一、单选题
-
1. 下列各数中最小的是( )A、0 B、 C、-3 D、﹣π2. 下列运算正确的是( )A、a2+3a3=4a5 B、(a+b)2=a2+b2 C、(b+a)(a-b)=a2-b2 D、(-3a3)2=6a63. 下图是由 个大小相同的小正方体组成的几何体,它的左视图是( )
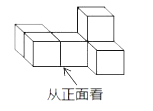 A、
A、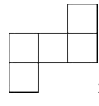 B、
B、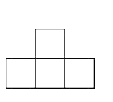 C、
C、 D、
D、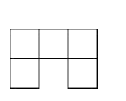 4. 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则 等于( )
4. 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则 等于( ) A、 B、 C、 D、5. 下列所述图形中,既是轴对称图形又是中心对称图形的是( )A、等腰三角形 B、等边三角形 C、菱形 D、平行四边形6. 抛物线y=(x﹣1)2+3关于x轴对称的抛物线的解析式是( )A、y=﹣(x﹣1)2+3 B、y=(x+1)2+3 C、y=(x﹣1)2﹣3 D、y=﹣(x﹣1)2﹣37. 如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )
A、 B、 C、 D、5. 下列所述图形中,既是轴对称图形又是中心对称图形的是( )A、等腰三角形 B、等边三角形 C、菱形 D、平行四边形6. 抛物线y=(x﹣1)2+3关于x轴对称的抛物线的解析式是( )A、y=﹣(x﹣1)2+3 B、y=(x+1)2+3 C、y=(x﹣1)2﹣3 D、y=﹣(x﹣1)2﹣37. 如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )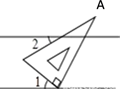 A、28° B、22° C、32° D、38°8. 如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )
A、28° B、22° C、32° D、38°8. 如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )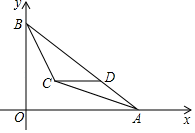 A、( ,2) B、( ,1) C、( ,2) D、( ,1)9. 如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2020次旋转结束时,点D的坐标为( )
A、( ,2) B、( ,1) C、( ,2) D、( ,1)9. 如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2020次旋转结束时,点D的坐标为( ) A、(﹣2,7) B、(7,2) C、(2,﹣7) D、(﹣7,﹣2)10. 如图,在R△ABC中,∠ACB=90°,AC=6,BC=8,E为AC上一点,且AE= ,AD平分∠BAC交BC于D.若P是AD上的动点,则PC+PE的最小值等于( )
A、(﹣2,7) B、(7,2) C、(2,﹣7) D、(﹣7,﹣2)10. 如图,在R△ABC中,∠ACB=90°,AC=6,BC=8,E为AC上一点,且AE= ,AD平分∠BAC交BC于D.若P是AD上的动点,则PC+PE的最小值等于( )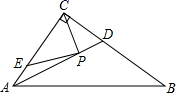 A、 B、 C、4 D、11. 如图,四边形 内接于 , , , ,弦 平分 ,则 的长是( )
A、 B、 C、4 D、11. 如图,四边形 内接于 , , , ,弦 平分 ,则 的长是( ) A、 B、 C、12 D、13
A、 B、 C、12 D、13二、填空题
-
12. 化简: ÷ = .13. 如图,PA切⊙O于点A , PC过点O且与⊙O交于B , C两点,若PA=6cm , PB=2 cm , 则△PAC的面积是cm2 .
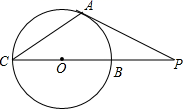 14. 如图,在平面直角坐标系中, 为坐标原点, 的边 在 轴上,顶点 在 轴的正半轴上,点 在第一象限,将 沿 轴翻折,使点 落在 轴上的点 处,点 恰好为 的中点, 与 交于点 .若 图象经过点 ,且 ,则 的值为.
14. 如图,在平面直角坐标系中, 为坐标原点, 的边 在 轴上,顶点 在 轴的正半轴上,点 在第一象限,将 沿 轴翻折,使点 落在 轴上的点 处,点 恰好为 的中点, 与 交于点 .若 图象经过点 ,且 ,则 的值为. 15. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .
15. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .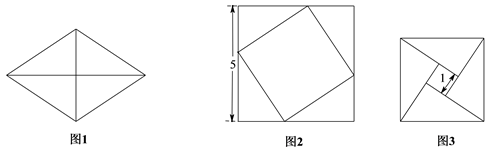
三、解答题
-
16. 按要求作答(1)、计算:|-6|- +(1- )0-(-3)(2)、解不等式组:17. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动,如图,在一个坡度(坡比 )的山坡 上发现一棵古树 ,测得古树低端C到山脚点A的距离 米,在距山脚点A水平距离 米的点 处,测得古树顶端D的仰角 (古树 与山坡 的剖面、点E在同一平面内,古树 与直线 垂直),求古树 的高度约为多少米? (结果保留一位小数,参考数据 )
 18. 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.
18. 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF. (1)、求证:DA=DE;(2)、如果AF∥CD,请判断四边形ADEF是什么特殊的四边形,并证明您的结论.19. 某学校有一批复印任务,原来由甲复印店承接,按每100页40元计费.现乙复印店表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印店每月收费情况如图所示.
(1)、求证:DA=DE;(2)、如果AF∥CD,请判断四边形ADEF是什么特殊的四边形,并证明您的结论.19. 某学校有一批复印任务,原来由甲复印店承接,按每100页40元计费.现乙复印店表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印店每月收费情况如图所示. (1)、乙复印店的每月承包费是多少元?(2)、当每月复印多少页时两复印店实际收费相同,费用是多少元?(3)、求甲、乙复印店的函数表达式.(4)、如果每月复印页数在1200页左右,那么应选择哪家复印店更合算.20. 某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
(1)、乙复印店的每月承包费是多少元?(2)、当每月复印多少页时两复印店实际收费相同,费用是多少元?(3)、求甲、乙复印店的函数表达式.(4)、如果每月复印页数在1200页左右,那么应选择哪家复印店更合算.20. 某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.组别
时间/小时
频数/人数
A组
2
B组
m
C组
10
D组
12
E组
7
F组
4
频数分布表
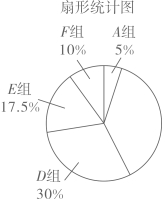
请根据图表中的信息解答下列问题:
(1)、求频数分布表中m的值;(2)、求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;(3)、已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生。21. 如图,在平面直角坐标系xOy中,抛物线y = ax2+ bx + c经过A、B、C三点,已知点A(-3,0),B(0,3),C(1,0). (1)、求此抛物线的解析式;(2)、点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;(3)、在直线x = -2上是否存在点M,使得∠MAC = 2∠MCA,若存在,求出M点坐标.若不存在,说明理由.
(1)、求此抛物线的解析式;(2)、点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;(3)、在直线x = -2上是否存在点M,使得∠MAC = 2∠MCA,若存在,求出M点坐标.若不存在,说明理由.