海南省海口市2020年数学中考三模试卷
试卷更新日期:2021-02-03 类型:中考模拟
一、单选题
-
1. 2020的倒数是( )A、 B、 C、 D、2. 下列计算正确的是( )A、a2+a3=a5 B、a2·a4=a8 C、a6÷a2=a3 D、(-2a3)2=4a63. 由 ,可得出 与 的关系是( )A、 B、 C、 D、4. 若反比例函数y= 的图象经过点(-3,4),则它的图象也一定经过的点是( )A、(-4,-3) B、(-3,-4) C、(2,-6) D、(6,2)5. 一个不等式组的解集在数轴上表示如图所示,则该不等式组的解集为( )
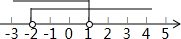 A、x>-2 B、x<1 C、-2≤x≤1 D、-2<x<16. 如图所示的几何体的主视图是( )
A、x>-2 B、x<1 C、-2≤x≤1 D、-2<x<16. 如图所示的几何体的主视图是( ) A、
A、 B、
B、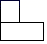 C、
C、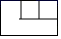 D、
D、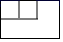 7. 近年来,“快递业”成为我国经济的一匹“黑马”,2017年我国快递业务量为400亿件,2019年快递量将达到600亿件,设快递量平均每年增长率为x,则下列方程中正确的是( )A、400(1+x)=600 B、400(1+2x)=600 C、400(1+x)2=600 D、600(1-x)2=4008. 如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于( )
7. 近年来,“快递业”成为我国经济的一匹“黑马”,2017年我国快递业务量为400亿件,2019年快递量将达到600亿件,设快递量平均每年增长率为x,则下列方程中正确的是( )A、400(1+x)=600 B、400(1+2x)=600 C、400(1+x)2=600 D、600(1-x)2=4008. 如图,在△ABC中,DE垂直平分AC,若BC=6,AD=4,则BD等于( )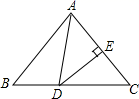 A、1.5 B、2 C、2.5 D、39. 将四边形纸片ABCD按如图的方式折叠使C′P∥AB.若∠B=120°,∠C=90°,则∠CPR等于( )
A、1.5 B、2 C、2.5 D、39. 将四边形纸片ABCD按如图的方式折叠使C′P∥AB.若∠B=120°,∠C=90°,则∠CPR等于( ) A、30° B、45° C、60° D、90°10. 如图,菱形ABCD的周长为20,对角线AC与BD交于点O,BD=6,则AC等于( )
A、30° B、45° C、60° D、90°10. 如图,菱形ABCD的周长为20,对角线AC与BD交于点O,BD=6,则AC等于( )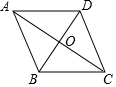 A、6 B、8 C、10 D、1211. 如图,△ABC是半径为1的⊙O的内接正三角形,则圆的内接矩形BCDE的面积为( )
A、6 B、8 C、10 D、1211. 如图,△ABC是半径为1的⊙O的内接正三角形,则圆的内接矩形BCDE的面积为( )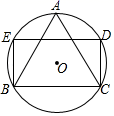 A、3 B、 C、 D、12. 小明要给刚结识的朋友小林打电话,他只记住了电话号码的前8位数字,后3位是3,6,8三个数字的某一种排列顺序,但具体顺序忘记了,那么小明第一次就拨通电话的概率是( )A、 B、 C、 D、
A、3 B、 C、 D、12. 小明要给刚结识的朋友小林打电话,他只记住了电话号码的前8位数字,后3位是3,6,8三个数字的某一种排列顺序,但具体顺序忘记了,那么小明第一次就拨通电话的概率是( )A、 B、 C、 D、二、填空题
-
13. 比较大小:5+ 3+ .14. 若代数式 和 的值相等,则x= .15. 如图,在△ABC中,AB=AC=8,点D是BC边上一点,且DE∥AC,DF∥AB,则四边形DEAF的周长为.
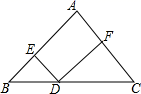 16. 如图是一个量角器和一个含30°的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半面O于点F,且BC=OE=2.若以O、B、F为顶点的三角形与△ABC相似,则OB的长为.
16. 如图是一个量角器和一个含30°的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半面O于点F,且BC=OE=2.若以O、B、F为顶点的三角形与△ABC相似,则OB的长为.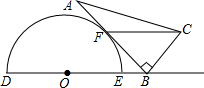
三、解答题
-
17. 计算与化简(1)、计算: ;(2)、先化简,再求值 ,其中a= .18. 某超市计划购进一批甲、乙两种玩具,已知 件甲种玩具的进价与 件乙种玩具的进价的和为 元, 件甲种玩具的进价与 件乙种玩具的进价的和为 元.(1)、求每件甲种、乙种玩具的进价分别是多少元;(2)、如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过 件,超出部分可以享受 折优惠,若购进 件甲种玩具需要花费 元,请你写出 与 的函数表达式.19. 某工厂甲、乙两个部门各有员工200人,为了了解这两个部门员工的生产技能情况,相关部门进行了抽样调查,过程如下:
(收集数据)从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制,单位:分)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
75
80
85
70
83
77
乙
92
71
83
81
72
81
91
83
75
82
80
81
69
81
73
74
82
80
70
59
(整理、描述数据)按分数段整理以上两组样本数据后,绘制甲、乙两部门员工成绩的频数分布图(如图)
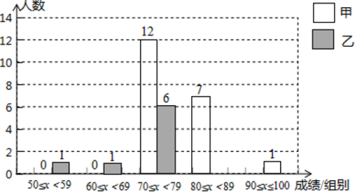
(说明:测试成绩80分及以上为优秀,70~79分为良好,60-69分为合格)
(分析数据)两组样本数据的平均数,中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.35
77.5
75
乙
(1)、请将上述不完整的频数分布图补充完整;(2)、请分别求出乙部门员工测试成绩的平均数,中位数和众数填入表中;(3)、请根据以上统计过程进行下列推断;①估计乙部门生产技能优秀的员工约有多少人;
②你认为甲,乙哪个部门员工的生产技能水平较高,请说明理由,(至少从两个不同的角度说明推晰的合理性)
20. 如图,小岛A在港口P的南偏西45方向,距离港口81海里处,甲船从A出发,沿AP方向以9海里时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里时的速度驶离港口,现两船同时出发,求出发后几小时乙船在甲船的正东方向(结果精确到0.1小时)(参考数据: =1.414, ≈1.72)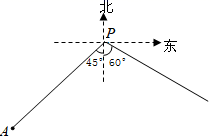 21. 如图1,矩形AEFG的两顶点E、G分别落在矩形ABCD的边BC和射线CD上,连结AC、FC,并过点F作FH⊥BC,交BC的延长线于点B
21. 如图1,矩形AEFG的两顶点E、G分别落在矩形ABCD的边BC和射线CD上,连结AC、FC,并过点F作FH⊥BC,交BC的延长线于点B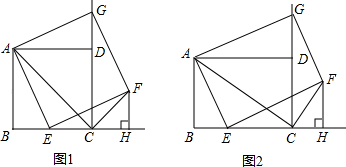 (1)、如图1,当AB=BC时,
(1)、如图1,当AB=BC时,①求证:△ABE≌△ADG;
②求证:矩形AEFG是正方形.
③猜想AC与FC的位置关系,并证明你的猜想.
(2)、如图2,当AB≠BC时,在(1)③中的猜想是否成立?若不成立,请说明理由;若成立,请给出证明.22. 如图1,抛物线与x轴交于A、B两点,与y轴交于点C(0,3),且OB=OC=3AO.直线y=x+1与抛物线交于A、D两点,与y轴交于点E.设直线AD上方的抛物线上的动点P的横坐标为t.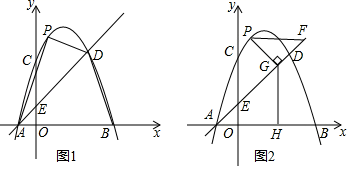 (1)、求该抛物线的表达式及点D的坐标;(2)、如图1,当t为何值时,S△PAD= S△DAB;(3)、如图2,过点P作PF∥x轴,交直线AD于点F,PG⊥AD于点G,GH⊥x轴于点H.
(1)、求该抛物线的表达式及点D的坐标;(2)、如图1,当t为何值时,S△PAD= S△DAB;(3)、如图2,过点P作PF∥x轴,交直线AD于点F,PG⊥AD于点G,GH⊥x轴于点H.①求△PFG的周长的最大值;
②当PF= GH时,求t的值.