海南省二十五校2020年数学7月模拟联考试卷
试卷更新日期:2021-02-03 类型:中考模拟
一、单选题
-
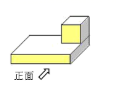
1. 下列运算正确的是( )A、 B、 C、 D、2. 数据160000000用科学记数法表示为A、 B、 C、 D、3. 要使式子 有意义,则x的取值范围是( )A、x>1 B、x>﹣1 C、x≥1 D、x≥﹣14. 如图是一个长方体上放着一个小正方体组成的立体图形,这个立体图形的左视图是( )
 A、
A、 B、
B、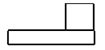 C、
C、 D、
D、 5. 甲、乙两所医院分别有一男一女共 名医护人员支援湖北武汉抗击疫情,若从甲、乙两医院支援的医护人员中分别随机选 名,则所选的 名医护人员性别相同的概率是( )A、 B、 C、 D、6. 在西线高铁工程中,某路段需铺轨.先由甲队独做 天后,再由乙队独做 天刚好完成.已知乙队单独完成比甲队单独完成多用 天,求甲、乙队单独完成各需要多少天?若设甲队单独完成需 天, 则所列方程正确的是( )A、 B、 C、 D、7. 含 角的直角三角板与直线 的位置关系如图 所示,已知 ,则 的度数是( )
5. 甲、乙两所医院分别有一男一女共 名医护人员支援湖北武汉抗击疫情,若从甲、乙两医院支援的医护人员中分别随机选 名,则所选的 名医护人员性别相同的概率是( )A、 B、 C、 D、6. 在西线高铁工程中,某路段需铺轨.先由甲队独做 天后,再由乙队独做 天刚好完成.已知乙队单独完成比甲队单独完成多用 天,求甲、乙队单独完成各需要多少天?若设甲队单独完成需 天, 则所列方程正确的是( )A、 B、 C、 D、7. 含 角的直角三角板与直线 的位置关系如图 所示,已知 ,则 的度数是( ) A、 B、 C、 D、8. 如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于( )
A、 B、 C、 D、8. 如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于( ) A、2 B、3 C、4 D、69. 如图,A,D是⊙O上的两个点,BC是直径,若∠D=34°,则∠OAC等于( )
A、2 B、3 C、4 D、69. 如图,A,D是⊙O上的两个点,BC是直径,若∠D=34°,则∠OAC等于( )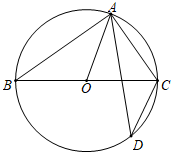 A、68° B、58° C、72° D、56°10. 如图,平面直角坐标系中,已知 ,将线段 绕点 顺时针旋转 得到线段 ,点 恰好在反比例函数 的图象上,则 等于( )
A、68° B、58° C、72° D、56°10. 如图,平面直角坐标系中,已知 ,将线段 绕点 顺时针旋转 得到线段 ,点 恰好在反比例函数 的图象上,则 等于( ) A、3 B、4 C、 D、811. 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()
A、3 B、4 C、 D、811. 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()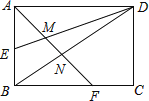
A、 B、 C、 D、二、填空题
-
12. 因式分解: .13. 如图 ,在 中, 于 ,点 为 的中点, ,则 的面积等于.
 14. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a2020=.15. 如图 ,在 中, ,点 为 边上一动点(不与点 重合),以点 为圆心, 的长为半径作 . 当 与 边相切时, 的长为.
14. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a2020=.15. 如图 ,在 中, ,点 为 边上一动点(不与点 重合),以点 为圆心, 的长为半径作 . 当 与 边相切时, 的长为.
三、解答题
-
16. 计算: ;
解不等式组: ;
17. 某文艺团体为“希望工程”募捐组织了一场义演,已知成人票每张8元,学生票每张5元,共售出1000张票,筹得票款6950元,求成人票与学生票各售出多少张.18. “停课不停学”期间,某校为了解学生每天在家体育活动的时间(单位: ),随机线上抽 查了该校的部分学生,对他们每天在家的体自活动时间进行调查,并将调查统计的结果分为四类:每天体育活动时间 分钟的学生记为 类, 分钟 分钟记为 类, 分钟 分钟记为 类, 分钟记为 类,收集的数据绘制如下两幅不完整的统计图, 请根据图中提供的信息,解答下列问题:
这次共抽取了_▲_名学生进行调查统计;
将条形统计图补充完整;
扇形统计图中 类所对应的扇形圆心角大小为_▲_ ;
如果该校共有 名学生,请你估计该校 类学生约有多少人?
19. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健 身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .填空: __▲_度;
求斜坡 的长.(结果保留根号).


