宁夏银川市永宁县2020届九年级数学第二次联考试卷
试卷更新日期:2021-02-03 类型:中考模拟
一、单选题
-
1. 下列计算正确的是 ( )A、 = B、 C、 D、 ( ≥0, >0)2. 如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是( )
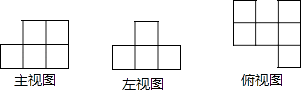 A、9 B、8 C、7 D、63. 把抛物线 向右平移1个单位,所得抛物线的函数表达式为A、 B、 C、 D、4. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
A、9 B、8 C、7 D、63. 把抛物线 向右平移1个单位,所得抛物线的函数表达式为A、 B、 C、 D、4. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁5. 已知菱形ABCD的周长是16,∠A=60°,则较短的对角线BD的长度为( )A、2 B、 C、4 D、6. 如图,AB是⊙O的直径,∠AOC=110°, 则∠D=( )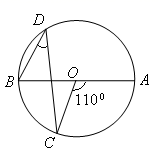 A、250 B、350 C、550 D、7007. 某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共有了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为A、 B、 C、 D、8. 函数 与 (k≠0)在同一直角坐标系中的图象可能是( )A、
A、250 B、350 C、550 D、7007. 某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共有了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为A、 B、 C、 D、8. 函数 与 (k≠0)在同一直角坐标系中的图象可能是( )A、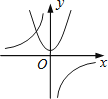 B、
B、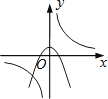 C、
C、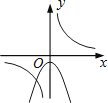 D、
D、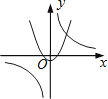
二、填空题
-
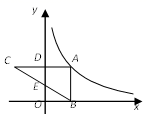
9. 因式分解:m3-4mn2 =.10. 两点在数轴上,点 对应的数为2.若线段 的长为5,则点 对应的数为.11. 已知x=1是一元二次方程x²+ax-b=0的一个根,则代数式a²+b²-2ab的值是.12. 某公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获利20%,则这种电子产品的标价为元.13. 一个不透明的袋子中有3个分别标有数字3,1,﹣2的球,这些球除所标的数字不同外其它都相同.若从袋子中随机摸出两个球,则这两个球上的两个数字之和为负数的概率是14. 已知扇形的面积是3πcm2 , 扇形的圆心角是120°,扇形的弧长是 cm(结果保留π).15. 如图,点A在反比例函数 (x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使AD=DC,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为4,则k的值为 .
 16. 如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 , AC=5,AD=4,则⊙O的直径AE= .
16. 如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 , AC=5,AD=4,则⊙O的直径AE= .
三、解答题
-
17. 解不等式组,并写出其整数解18. 先化简,再求值: ,其中19. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).

①先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1 , 请画出△A1B1C1;
②将△A1B1C1绕B1点顺时针旋转90°,得△A2B2C2 , 请画出△A2B2C2;
20. 李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.制成以下两幅不完整的统计图,请你根据统计图解答下列问题: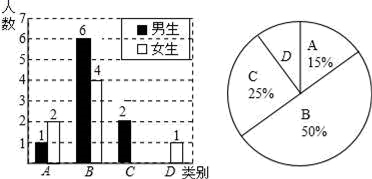 (1)、李老师一共调查了多少名同学?(2)、C类女生有多少名,D类男生有多少名,将下面条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.21. 为了巩固全国文明城市建设成果,突出城市品质的提升,近年来,我市积极落实节能减排政策,推行绿色建筑,据统计,我市2016年的绿色建筑面积约为950万平方米,2018年达到了1862万平方米.若2017年、2018年的绿色建筑面积按相同的增长率逐年递增,请解答下列问题:(1)、求这两年我市推行绿色建筑面积的年平均增长率;(2)、2019年我市计划推行绿色建筑面积达到2400万平方米.如果2019年仍保持相同的年平均增长率,请你预测2019年我市能否完成计划目标?22. 如图,在▱ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)、李老师一共调查了多少名同学?(2)、C类女生有多少名,D类男生有多少名,将下面条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.21. 为了巩固全国文明城市建设成果,突出城市品质的提升,近年来,我市积极落实节能减排政策,推行绿色建筑,据统计,我市2016年的绿色建筑面积约为950万平方米,2018年达到了1862万平方米.若2017年、2018年的绿色建筑面积按相同的增长率逐年递增,请解答下列问题:(1)、求这两年我市推行绿色建筑面积的年平均增长率;(2)、2019年我市计划推行绿色建筑面积达到2400万平方米.如果2019年仍保持相同的年平均增长率,请你预测2019年我市能否完成计划目标?22. 如图,在▱ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD. (1)、求证:△ABE≌△CDF;(2)、若AB=DB,求证:四边形DFBE是矩形.23. AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
(1)、求证:△ABE≌△CDF;(2)、若AB=DB,求证:四边形DFBE是矩形.23. AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.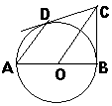 (1)、求证:DC为⊙O切线;(2)、若AD·OC=8,求⊙O半径.24. 如图所示,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(-2,0).
(1)、求证:DC为⊙O切线;(2)、若AD·OC=8,求⊙O半径.24. 如图所示,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(-2,0). (1)、求双曲线的解析式;(2)、若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角与△AOB相似时,求点Q的坐标.25. 在国道202公路改建工程中,某路段长4000米,由甲乙两个工程队拟在30天内(含30天)合作完成,已知两个工程队各有10名工人(设甲乙两个工程队的工人全部参与生产,甲工程队每人每天的工作量相同,乙工程队每人每天的工作量相同),甲工程队1天、乙工程队2天共修路200米;甲工程队2天,乙工程队3天共修路350米.(1)、试问甲乙两个工程队每天分别修路多少米?(2)、甲乙两个工程队施工10天后,由于工作需要需从甲队抽调m人去学习新技术,总部要求在规定时间内完成,请问甲队可以抽调多少人?(3)、已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,甲乙两队需各做多少天?最低费用为多少?26. 已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.(1)、当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(1)、求双曲线的解析式;(2)、若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角与△AOB相似时,求点Q的坐标.25. 在国道202公路改建工程中,某路段长4000米,由甲乙两个工程队拟在30天内(含30天)合作完成,已知两个工程队各有10名工人(设甲乙两个工程队的工人全部参与生产,甲工程队每人每天的工作量相同,乙工程队每人每天的工作量相同),甲工程队1天、乙工程队2天共修路200米;甲工程队2天,乙工程队3天共修路350米.(1)、试问甲乙两个工程队每天分别修路多少米?(2)、甲乙两个工程队施工10天后,由于工作需要需从甲队抽调m人去学习新技术,总部要求在规定时间内完成,请问甲队可以抽调多少人?(3)、已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,甲乙两队需各做多少天?最低费用为多少?26. 已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.(1)、当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明; (2)、在(1)的条件下,若DE:AE:CE=1: :3,求∠AED的度数;(3)、若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF= ,求CN的长.
(2)、在(1)的条件下,若DE:AE:CE=1: :3,求∠AED的度数;(3)、若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF= ,求CN的长.