宁夏银川市永宁县2020届九年级数学第一次联考试卷

试卷更新日期：2021-02-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 新型冠状病毒感染肺炎疫情发生后，医用酒精作为必不可少的消毒用品，发挥着巨大的作用，如图是医用酒精瓶的示意图，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 某种冠状病毒的直径120纳米，1纳米 $= 10^{- 9}$ 米，则这种冠状病毒的直径（单位是米）用科学记数法表示为（）

A、 $120 \times 10^{- 9}$ 米 B、 $1.2 \times 10^{- 8}$ 米 C、 $1.2 \times 10^{- 7}$ 米 D、 $1.2 \times 10^{- 6}$ 米

查看试题解析

4. 永宁县某中学在预防“新冠肺炎”期间，要求学生每日测量体温，九（5）班一名同学连续一周体温情况如下表所示：则该名同学这一周体温数据的众数和中位数分别是（）

日期	星期一	星期二	星期三	星期四	星期五	星期六	星期天
体温（℃）	36.2	36.2	36.5	36.3	36.2	36.4	36.3

A、36.3和36.2 B、36.2和36.3 C、36.2和36.2 D、36.2和36.1

查看试题解析

5. 如果关于x的一元二次方程kx²﹣4x-1=0有实数根，那么k应满足的条件是（）

A、k＞-4 B、 $k \geq - 4$ 且 $k \neq 0$ C、 $k > - 4$ 且 $k \neq 0$ D、k≤1

查看试题解析
6. 如图，四边形ABCD内接于⊙O，DA=DC，∠CBE=50°，则∠DAC的大小为（）

A、65° B、50° C、72° D、60°

查看试题解析
7. 如图，在已知的△ABC中，按以下步骤作图：①分别以B、C为圆心，以大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于点M、N；②作直线MN交AB于点D，连接CD，若CD＝AD，∠B＝20°，则下列结论中错误的是（　　）

A、∠CAD＝40° B、∠ACD＝70° C、点D为△ABC的外心 D、∠ACB＝90°

查看试题解析
8. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 3$ ，动点 $P$ 沿折线 $B C D$ 从点 $B$ 开始运动到点 $D$ ．设运动的路程为 $x$ ， $Δ A D P$ 的面积为 $y$ ，那么 $y$ 与 $x$ 之间的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算： $a^{2} \cdot a^{3} =$ .

查看试题解析
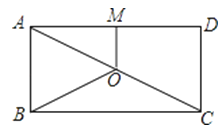
10. 分解因式：x²y+2xy+y= ．

查看试题解析
11. 某正多边形的边心距为 $2 \sqrt{2}$ ，半径为4，则该正多边形的面积为.

查看试题解析
12. 不等式组 ${\begin{array}{l} 2 x > 3 x \\ x + 4 > 2 \end{array}$ 的整数解是.

查看试题解析
13. 若点 $(- 1, y_{1}), (2, y_{2}), (3, y_{3})$ 在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上，则 $y_{1}, y_{2}, y_{3}$ 的大小关系是.

查看试题解析
14.
如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB=5，AD=12，则四边形ABOM的周长为．

查看试题解析
15. 定义：等腰三角形的顶角与其一个底角的度数的比值 $k$ 称为这个等腰三角形的“特征值”.若等腰 $△ A B C$ 中， $∠ A = 80 °$ ，则它的特征值 $k =$ .

查看试题解析
16. 如图，菱形ABCD的边长为4cm，∠A＝60°，弧BD是以点A为圆心，AB长为半径的弧，弧CD是以点B为圆心，BC长为半径的弧，则阴影部分的面积为.

查看试题解析

三、解答题

17. 计算： $\sqrt{27} + {(- \frac{1}{2})}^{- 2} - 3 \tan 60^{°} + {(π - \sqrt{2})}^{0}$

查看试题解析
18. 解方程： $\frac{x}{x + 1} + \frac{2}{x} = 1$

查看试题解析
19. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）.

(1)、①画出△ABC关于y轴对称的图形△A₁B₁C₁ ，并直接写出C₁点的坐标；
②以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A₂B₂C₂ ，并直接写出C₂点坐标；

(2)、如果点D（a，b）在线段AB上，请直接写出经过（2）的变化后D的对应点D₂的坐标.

查看试题解析

20. 为了展现新时代青年学子勇于担当的责任感和强烈的爱国情怀，自治区教育工委、教育厅组织开展了全区学生“共抗疫情、爱国力行”网络文化作品征集展示活动，现将从中挑选的50件参赛作品的成绩（单位：分）统计如下：

等级	成绩（用m表示）	频数	频率
A	$90 \leq m \leq 100$	$x$	0.08
B	$80 \leq m < 90$	34	$y$
C	$m < 80$	12	0.24
合计		50	1

请根据上表提供的信息，解答下列问题：

(1)、表中x的值为， y的值为（直接填写结果）

(2)、将本次参赛作品获得A等级的学生依次用A₁、A₂、A₃表示.若从本次参赛作品获得A等级的学生中，随机抽取两名学生谈谈他们的参赛体会，用列表或画树状图的方法，求恰好抽到学生A₁和A₂概率.

查看试题解析

21. 如图，在平行四边形ABCD中，AE平分∠DAB，已知CE=6，BE=8，DE=10.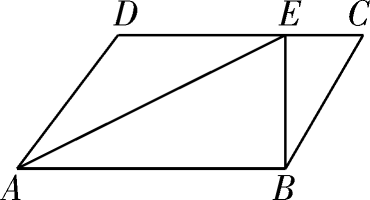

(1)、求证：∠BEC=90°；

(2)、求cos∠DAE.

查看试题解析
22. 永宁县某中学在疫情复学准备工作中，为了贯彻落实“生命重于泰山、疫情就是命令、防控就是责任”的思想，计划购买500瓶消毒液，已知甲种消毒液每瓶50元，乙种消毒液每瓶30元.

(1)、若该学校购买两种消毒液共花费19000元，则购买甲、乙两种消毒液各多少瓶？

(2)、若计划购买两种消毒液的总费用不超过20000元，则最多购买甲种消毒液多少瓶？

查看试题解析
23. 如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．

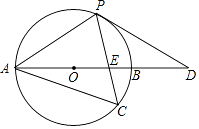(1)、试判断PD与⊙O的位置关系，并说明理由；

(2)、若点C是弧AB的中点，已知AB=4，求CE•CP的值．

查看试题解析
24. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象与反比例函数 $y = \frac{m^{2} - 3 m}{x}$ （ $m \neq 0$ 且 $m \neq 3$ ）的图象在第一象限交于点 $A$ 、 $B$ ，且该一次函数的图象与 $y$ 轴正半轴交于点 $C$ ，过 $A$ 、 $B$ 分别作 $y$ 轴的垂线，垂足分别为 $E$ 、 $D$ .已知 $A (4 ， 1)$ ， $C E = 4 C D$ .

(1)、求 $m$ 的值和反比例函数的解析式；

(2)、若点 $M$ 为一次函数图象上的动点，求 $O M$ 长度的最小值.

查看试题解析
25. 某县积极响应市政府加大产业扶贫力度的号召，决定成立草莓产销合作社，负责扶贫对象户种植草莓的技术指导和统一销售，所获利润年底分红.经市场调研发现，草莓销售单价 $y$ （万元）与产量x（吨）之间的关系如图所示 $(0 \leq x \leq 100)$ .已知草莓的产销投入总成本 $p$ （万元）与产量x $x$ （吨）之间满足 $p = x + 1$ .

(1)、直接写出草莓销售单价 $y$ （万元）与产量 $x$ （吨）之间的函数关系式；

(2)、求该合作社所获利润 $w$ （万元）与产量 $x$ （吨）之间的函数关系式；

(3)、为提高农民种植草莓的积极性，合作社决定按 $0.3$ 万元/吨的标准奖励扶贫对象种植户，为确保合作社所获利润 $w^{'}$ （万元）不低于 $55$ 万元，产量至少要达到多少吨？

查看试题解析
26.
如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．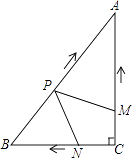

(1)、当t为何值时，以A，P，M为顶点的三角形与△ABC相似？

(2)、是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

查看试题解析