宁夏吴忠市盐池县2020届数学中考一模试卷

试卷更新日期：2021-02-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各点中，在函数y=－ $\frac{8}{x}$ 图象上的是（）

A、（﹣2，4） B、（2，4） C、（﹣2，﹣4） D、（8，1）

查看试题解析
2. 已知△ABC∽△DEF，AB：DE=1：2，则△ABC与△DEF的周长比等于（）

A、2：1 B、4：1 C、1：2 D、1：4

查看试题解析
3. 在 $△ A B C$ 中，∠C＝90°，AC＝6，AB＝10，则tanA的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析
4. 已知cosα＝ $\frac{1}{2}$ ，锐角α的度数是（）

A、30° B、45° C、60° D、以上度数都不对

查看试题解析
5. 点A(－1，y₁)，B(－2，y₂)在反比例函数y＝ $\frac{2}{x}$ 的图象上，则y₁ ， y₂的大小关系是（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、不能确定

查看试题解析
6. 已知在 $R t △ A B C$ 中，∠C＝90°，AB＝13，AC＝12，则∠B的余弦值为（）

A、 $\frac{12}{13}$ B、 $\frac{5}{13}$ C、 $\frac{5}{12}$ D、 $\frac{12}{5}$

查看试题解析
7. 如图，在等腰 $R t △ A B C$ 中，∠C＝90°，AC＝6，D是AC上一点，若tan∠DBA＝ $\frac{1}{5}$ ，则AD的长为（）

A、3 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、2

查看试题解析
8. 关于x的函数y＝k（x＋1）和y＝ $\frac{k}{x}$ （k≠0）在同一坐标系中的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 已知sinA= $\frac{1}{2}$ ，则锐角∠A=.

查看试题解析
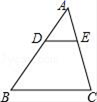
10. 已知 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ 且 $\frac{A B}{A^{'} B^{'}}$ ＝ $\frac{1}{2}$ ，则 $S_{△ A B C} ∶ S_{△ A^{'} B^{'} C^{'}}$ 为

查看试题解析
11. 反比例函数y＝ $\frac{m - 1}{x}$ 的图象在第一、三象限，则m的取值范围是．

查看试题解析
12. 如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E.若AD=1，DB=2，则△ADE的面积与△ABC的面积的比等于.

查看试题解析
13. 如图是教学用直角三角板，边AC＝30 cm，∠C＝90°，tan∠BAC＝ $\frac{\sqrt{3}}{3}$ ，则边BC的长为

查看试题解析
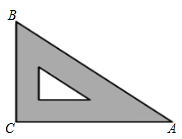14. 一菱形的面积为12cm² ，它的两条对角线长分别为acm，bcm，则a与b之间的函数解析式为a＝ $\frac{24}{b}$ （b＞0）；这个函数的图象位于第象限.

查看试题解析
15. 反比例函数 $y = \frac{k}{x}$ 的图象经过点（tan45°，cos60°），则k＝.

查看试题解析
16. 如图，在 $Δ A B C$ 中，D、E分别是边 $A B$ 、 $A C$ 上的点，且 $D E$ ∥ $B C$ ，若 $Δ A D E$ 与 $Δ A B C$ 的周长之比为 $2 ： 3$ ，AD=4，则DB=.

查看试题解析
17. 如图，为了测量某棵树的高度，小明用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点.此时，竹竿与这一点距离相距6m，与树相距15m，则树的高度为m

查看试题解析
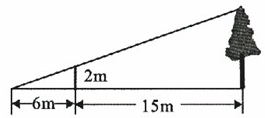18. 如图，已知E是平行四边形ABCD的一边AD延长线上的一点，AD＝3DE，则DF＝AB.

查看试题解析

三、解答题

19. 按要求作答

(1)、计算： $\frac{\sin 60^{°}}{\cos 30^{°}}$ －tan45°的值是多少？

(2)、已知点P（1，2）在反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象上.当x＝－2时，求y的值；

查看试题解析
20. 如图，A，B两点被池塘隔开，在AB外取一点C，连接AC，BC，在AC上取点M，使AM＝3MC，作MN∥AB交BC于点N，量得MN＝38m，求AB的长.

查看试题解析
21. 如图，正比例函数y＝kx（k>0）与反比例函数y＝ $\frac{4}{x}$ 的图象相交于A，C两点，过点A作x轴的垂线交x轴于点B，连接BC，则 $△ A B C$ 的面积等于多少？

查看试题解析
22. 如图，拦水坝的横断面为梯形ABCD，坝顶宽AD=5米，斜坡AB的坡度i=1：3（指坡面的铅直高度AE与水平宽度BE的比），斜坡DC的坡度i=1：1.5，已知该拦水坝的高为6米．

(1)、求斜坡AB的长；

(2)、求拦水坝的横断面梯形ABCD的周长．
（注意：本题中的计算过程和结果均保留根号）

查看试题解析
23. 如图所示，已知在Rt△ABC中，∠C＝90°，D是BC边上的一点，AC＝2，CD＝1，记∠CAD＝α.

(1)、试写出α的三个三角函数值；

(2)、若∠B＝α，求BD的长.

查看试题解析
24. 如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心，支架CD与水平面AE垂直，AB=150厘米，∠BAC=30°，另一根辅助支架DE=76厘米，∠CED=60°.

(1)、求垂直支架CD的长度.（结果保留根号）

(2)、求水箱半径OD的长度.（结果精确到0.1，参考数据：，）

查看试题解析
25. 如图，一次函数y=kx+b与反比例函数 $y = \frac{6}{x} (x > 0)$ 的图象交于A（m，6），B（3，n）两点．

(1)、求一次函数的解析式；

(2)、根据图象直接写出 $k x + b - \frac{6}{x} < 0$ 的x的取值范围；

(3)、求△AOB的面积．

查看试题解析