湖北省宜城市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、单选题

1. 如果一个物体向右移动2米记作移动+2米，那么这个物体又移动了-2米的意思是（）

A、物体又向右移动了2米 B、物体又向右移动了4米 C、物体又向左移动了2米 D、物体又向左移动了4米

查看试题解析
2. 计算 $- 2 - | - 3 |$ 的结果为（）

A、-5 B、-1 C、1 D、5

查看试题解析
3. 平方等于9的数是（）

A、±3 B、3 C、-3 D、±9

查看试题解析
4. 一天有 $8.64 \times 10^{4}$ 秒，一年按365天计算，一年有（）秒

A、 $3.1536 \times 10^{4}$ B、 $3.1536 \times 10^{5}$ C、 $3.1536 \times 10^{6}$ D、 $3.1536 \times 10^{7}$

查看试题解析
5. 下列说法错误的是（）

A、 $- 15 a b$ 的系数是 $- 15$ B、 $\frac{3 x^{2} y}{5}$ 的系数是 $\frac{1}{5}$ C、 $4 a^{2} b^{2}$ 的次数是4 D、 $a^{4} - 2 a^{2} b^{2} + b^{4}$ 的次数是4

查看试题解析
6. 下列去括号正确的是（）．

A、－2(a＋b)＝－2a＋b B、－2(a＋b)＝－2a－b C、－2(a＋b)＝－2a－2b D、－2(a＋b)＝－2a＋2b

查看试题解析
7. 长方形的长是 $3 x$ ，宽是 $2 x - y$ ，则长方形的周长是（）

A、 $10 x - 2 y$ B、 $10 x + 2 y$ C、 $6 x - 2 y$ D、 $10 x - y$

查看试题解析
8. 下列方程，是一元一次方程的是（）

A、 $a^{2} - 4 a = 3$ B、 $3 a - 1 = \frac{a}{2}$ C、 $a + 2 b = 1$ D、 $a b - 3 = 5$

查看试题解析
9. 已知等式 $3 x = 2 y + 3$ ，则下列变形不一定成立的是（）

A、 $3 x - 3 = 2 y$ B、 $x = \frac{2}{3} y + 1$ C、 $3 x + 1 = 2 y + 4$ D、 $3 x z = 2 y z + 5$

查看试题解析
10. 一商店在某一时间以每件60元的价格卖出两件衣服，其中一件盈利25%，另一件亏损20%，这家商店（）

A、亏损3元 B、盈利3元 C、亏损8元 D、不赢不亏

查看试题解析
11. 下列说法中错误的是（）

A、线段 $A B$ 和射线 $A B$ 都是直线的一部分 B、直线 $A B$ 和直线 $B A$ 是同一条直线 C、射线 $A B$ 和射线 $B A$ 是同一条射线 D、线段 $A B$ 和线段 $B A$ 是同一条线段

查看试题解析
12. 已知 $∠ α$ 的补角的一半比 $∠ α$ 小30°，则 $∠ α$ 等于（）

A、50° B、60° C、70° D、80°

查看试题解析

二、填空题

13. 数轴上表示数－5和表示－14的两点之间的距离是．

查看试题解析
14. 已知代数式 $a^{2} - 2 a$ 的值是-4，则代数式 $1 + 3 a^{2} - 6 a$ 的值是．

查看试题解析
15. 若单项式 $5 a^{m + 1} b$ 和 $25 a^{4} b^{n - 1}$ 是同类项，则 $m^{n}$ 的值为．

查看试题解析
16. 若方程 $6 x + 2 = 0$ 的解与关于 $y$ 的方程 $3 y + m = 15$ 的解互为相反数，则 $m =$ ．

查看试题解析
17. 已知 $A$ ， $B$ ， $C$ 三点在同一条直线上，且 $A B = 5 c m$ ， $B C = 2 c m$ ，则 $A C =$ $c m$ .

查看试题解析
18. 南偏东50°的射线与西南方向的射线组成的角（小于平角）的度数是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\frac{5}{7} \div (- 2 \frac{2}{5}) - \frac{5}{7} \times \frac{5}{12} - \frac{5}{3} \div 4$

(2)、 ${(- 2)}^{2} \times 5 - {(- 2)}^{3} \div 4 + 3^{2} \times (1 - 3)$

查看试题解析
20. 解方程：

(1)、 $2 x - (x + 10) = 5 x + 2 (x - 1)$

(2)、 $\frac{1 - 2 x}{3} = \frac{3 x + 1}{7} - 3$

查看试题解析
21. 化简求值： $3 x^{2} - [5 x - (\frac{1}{2} x - 3) + 2 x^{2}]$ ，其中 $x = 4$ ．

查看试题解析
22. 如图， $B D$ 平分 $∠ A B C$ ， $B E$ 把 $∠ A B C$ 分成的两部分 $∠ A B E ： ∠ E B C = 2 ： 5$ ， $∠ D B E = 21^{\circ}$ ，求 $∠ A B C$ 的度数．

查看试题解析
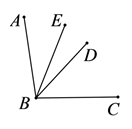23. 机械厂加工车间有85名工人，平均每人每天加工大齿轮16个或小齿轮10个，2个大齿轮和3个小齿轮配成一套，问需分别安排多少名工人加工大、小齿轮，才能使每
天加工的大小齿轮刚好配套？

查看试题解析
24. 如图，点 $A 、 B$ 都在数轴上， $O$ 为原点．

(1)、点 $B$ 表示的数是；

(2)、若点 $B$ 以每秒3个单位长度的速度沿数轴运动，则1秒后点 $B$ 表示的数是；

(3)、若点 $A 、 B$ 都以每秒3个单位长度的速度沿数轴向右运动，而点 $O$ 不动， $t$ 秒后有一个点是一条线段的中点，求 $t$ 的值．

查看试题解析
25. 用“※”定义一种新运算：对于任意有理数 $a$ 和 $b$ ，规定 $a ※ b = a b^{2} + 2 a b + a$ ．如 $1 ※ 3 = 1 \times 3^{2} + 2 \times 1 \times 3 + 1 = 16$ ．

(1)、求 $3 ※ (- 2)$ 的值；

(2)、若 $(\frac{a + 1}{2} ※ 3) ※ (- \frac{1}{2}) = 4$ ，求 $a$ 的值．

查看试题解析
26. 小刚和小强从 $A ， B$ 两地同时出发，小刚骑自行车，小强步行，沿同一条路线相向匀速而行．出发后两小时两人相遇，相遇时小刚比小强多行进24千米．相遇后0.5小时小刚到达 $B$ 地．

(1)、两人的行进速度分别是多少？

(2)、相遇后经过多少时间小强到达 $A$ 地？

(3)、 $A B$ 两地相距多少千米？

查看试题解析
27. 如图①，点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，将一直角三角板如图摆放（ $∠ M O N = 90^{\circ}$ ）．

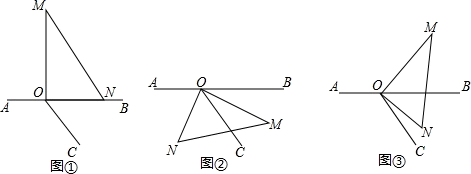(1)、若 $∠ B O C = 35^{\circ}$ ，求 $∠ M O C$ 的大小．

(2)、将图①中的三角板绕点 $O$ 旋转一定的角度得图②，使边 $O M$ 恰好平分 $∠ B O C$ ，问： $O N$ 是否平分 $∠ A O C$ ？请说明理由．

(3)、将图①中的三角板绕点 $O$ 旋转一定的角度得图③，使边 $O N$ 在 $∠ B O C$ 的内部，如果 $∠ B O C = 50^{\circ}$ ，则 $∠ B O M$ 与 $∠ N O C$ 之间存在怎样的数量关系？请说明理由．

查看试题解析