湖北省宜昌市五峰土家族自治县2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、单选题

1. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作+100元．那么﹣80元表示（）

A、支出20元 B、收入20元 C、支出80元 D、收入80元

查看试题解析
2. 近年来，中国高铁发展迅速，高铁技术不断走出国门，成为展示我国实力的新名片.现在中国高速铁路营运里程将达到23000公里，将23000用科学记数法表示应为（）

A、 $2.3 \times 10^{4}$ B、 $23 \times 10^{3}$ C、 $2.3 \times 10^{3}$ D、 $0.23 \times 10^{5}$

查看试题解析
3. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“爱”字一面的相对面上的字是（）

A、美 B、丽 C、五 D、峰

查看试题解析
4. 下列说法正确的是（）

A、单项式3ab的次数是1 B、3a－2a $^{2}$ b+2ab是三次三项式 C、单项式 $\frac{2 a b}{3}$ 的系数是2 D、－4a $^{2}$ b，3ab ， 5是多项式－4a $^{2}$ b+3ab-5的项

查看试题解析
5. 有理数a、b在数轴上的对应的位置如图所示，则正确的是（）

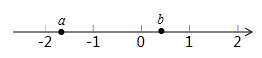A、a＋b＞0 B、a＋b＜0 C、a－b＝0 D、a－b＞0

查看试题解析
6. 下列各式计算正确的是 ( )

A、6a+a=6a² B、-2a+5b=3ab C、4m²n-2mn²=2mn D、3ab²-5b²a=-2ab²

查看试题解析
7. 如果线段AB=13cm，MA+MB=17 cm，那么下面说法中正确的是（）.

A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上，也可能在直线AB外

查看试题解析
8. 若方程3x+2a=12的解为x=8，则a的值为（）

A、6 B、8 C、－6 D、4

查看试题解析
9. 1261年，我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律，比欧洲的相同发现要早三百多年，我们把这个三角形称为“杨辉三角”，请观察图中的数字排列规律，则a，b，c的值分别为（）

A、 a=1，b=6，c=15 B、a=6，b=15，c=20 C、a=15，b=20，c=15 D、a=20，b=15，c=6

查看试题解析
10. 如图，下列说法不正确的是（）

A、OC的方向是南偏东30° B、OA的方向是北偏东45° C、OB的方向是西偏北30° D、∠AOB的度数是75°

查看试题解析

二、填空题

11. 商店上月收入为a元，本月比上月的2倍还多8元，本月的收入为元（用含a的式子表示）．

查看试题解析
12. 把一根木条钉牢在墙壁上需要个钉子，其理论依据是：

查看试题解析
13. 一个长方形的周长为 $6 a + 8 b$ ，其一边长为 $2 a + 3 b$ ，则另一边长为.

查看试题解析
14. 如图，已知线段AB=10cm，点N在线段AB上，NB=2cm，M是AB中点，那么线段MN的长为．

查看试题解析
15. 把一些图书分给某班学生阅读，若每人分3本，则剩余20本；若每人分4本，则还缺25本．这个班有多少学生？设这个班有x名学生，则由题意可列方程．

查看试题解析

三、解答题

16. 计算：

(1)、 $[(- 5) - (- 8)] + (- 4)$ ；

(2)、 ${-5}^{2} - [{(-2)}^{3} + | 1-0 .8 \times \frac{3}{4} | \div (-2)]$ .

查看试题解析
17. 解下列方程:

(1)、 $x + 6 = 1 - x$ ；

(2)、 $\frac{x + 1}{4} - 1 = \frac{2 x - 1}{6}$ .

查看试题解析
18. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - (a b^{2} + 3 a^{2} b)$ ，其中 $a = \frac{1}{2}$ ， $b = - \frac{1}{3}$

查看试题解析
19. 如图，平面上有四个点A、B、C、D：

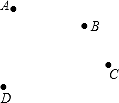(1)、根据下列语句画图：
①射线BA；

②直线BD与线段AC相交于点E；

(2)、图中以E为顶点的角中，请写出∠AED的补角。

查看试题解析
20. 看图：

(1)、如图1， $∠ AOD- ∠ A O C =$ ；

(2)、如图2， $∠ AOC$ 与 $∠ BOD$ 均为直角，当 $∠ B O C = 64 °$ 时，求 $∠ COD 、 ∠ AOD$ 的度数.

查看试题解析
21. 某市场的公平秤如图，把10千克的菜放到秤上，指示盘上的指针转了180°.

(1)、如果把2.75千克的菜放在秤上，指针转过多少度?

(2)、如果称好0.5千克的菜没有拿走，再把一捆菜放在秤上，指针共转了 $72 ° 54^{'} ，$ 那么，后放上的这捆菜有多少千克?

查看试题解析

22. “水是生命之源”，某市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：

用水量/月	单价(元/m³)
不超过20m³	2.8
超过20m³的部分	3.8
另：每立方米用水加收0.2元的城市污水处理费

(1)、根据上表，用水量每月不超过20m³,实际每立方米收水费元;如果1月份某用户用水量为19m³ ，那么该用户1月份应该缴纳水费元;

(2)、某用户2月份共缴纳水费80元，那么该用户2月份用水多少m³？

(3)、若该用户水表3月份出了故障，只有70%的用水量记入水表中，这样该用户在3月份只缴纳了58.8元水费，问该用户3月份实际应该缴纳水费多少元？

查看试题解析

23. 如图，点C在线段AB上，M、N分别是线段AC、BC的中点，

(1)、若AC=7cm，BC=5cm，求线段MN的长；

(2)、若AB=a，点C为线段AB上任意一点，你能用含a的代数式表示MN的长度吗？若能，请写出结果与过程，若不能，请说明理由；

(3)、若将（2）中“点C为线段AB上任意一点”改为“点C为直线AB上任意一点”，其余条件不变，（2）中的结论是否仍然成立？请画图并写出说明过程．

查看试题解析
24. 已知：OB、OC、OE是∠AOD内的射线，若∠AOD＝130°.

(1)、如图1，OB是∠AOC的平分线，OE是∠COD的平分线，∠BOE=度；

(2)、OF也是∠AOD内的射线，如图2，若∠FOC=20°，OB平分∠AOF，OE平分∠COD，当射线OC绕点O在∠AOF内旋转时，求∠BOE的大小；

(3)、在(2)的条件下，当射线OC从边OA开始绕O点以每秒2°的速度逆时针旋转t秒，如图3，若∠AOB：∠DOE=2：3，求t的值.

查看试题解析