湖北省武汉市青山区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、单选题
-
1. ﹣6的相反数是( )A、﹣6 B、﹣ C、6 D、2. 下列方程,是一元一次方程的是( )A、 B、 C、 D、3. 下列四个立体图形中,从正面看的图形为等腰三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如果x=1是关于x的方程5x+2m﹣7=0的解,那么m的值是( )A、﹣1 B、1 C、6 D、﹣65. 下列等式变形,正确的是( )A、由2+x=8得x=8+2 B、由2x+6=4x得x+6=2x C、由2x=3得x= D、由 −1=1得x−5=16. 如图,下列说法错误的是( )
4. 如果x=1是关于x的方程5x+2m﹣7=0的解,那么m的值是( )A、﹣1 B、1 C、6 D、﹣65. 下列等式变形,正确的是( )A、由2+x=8得x=8+2 B、由2x+6=4x得x+6=2x C、由2x=3得x= D、由 −1=1得x−5=16. 如图,下列说法错误的是( ) A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为7. 下列说法中,正确的是( )A、画直线 B、射线 与射线 是同一条射线 C、绝对值等于它本身的数是正数 D、多项式 是五次三项式8. 定义: “*”运算为“ ”,若 , 则 的值为( )A、1 B、 C、 D、29. 如图,是一个正方体的表面展开图, ,且相对两个面所表示的代数式的和都相等,则 代表的代数式是( )
A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为7. 下列说法中,正确的是( )A、画直线 B、射线 与射线 是同一条射线 C、绝对值等于它本身的数是正数 D、多项式 是五次三项式8. 定义: “*”运算为“ ”,若 , 则 的值为( )A、1 B、 C、 D、29. 如图,是一个正方体的表面展开图, ,且相对两个面所表示的代数式的和都相等,则 代表的代数式是( )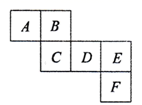 A、 B、10 C、 D、10. 如图, 分别平分 平分 ,下列结论:① ;② ;③ ;④ 其中正确的个数有( )
A、 B、10 C、 D、10. 如图, 分别平分 平分 ,下列结论:① ;② ;③ ;④ 其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是.12. 中国的陆地面积约为9 600 000km2 , 把9 600 000用科学记数法表示为 .13. .14. 已知角 的余角比它的补角的一半还少20°,则 °.15. 已知,线段 上有 两点, 点 为 中点,则 =.16. 双11电商节,某商店把某种商品按进价加20%作为定价,按定价的1.5倍标价再8折出售,最终售出10件,总营业额为720元,则这次生意的赢亏情况为元.
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 根据下列语句,画出图形.
 (1)、如图1,已知 四点.
(1)、如图1,已知 四点.①画直线 ;
②连接线段 ,相交于点 ;
③画射线 ,相交于点 .
(2)、如图2,有一个灯塔分别位于海岛 的南偏西30°和海岛 的南偏西60°的方向上,通过画图可推断灯塔的位置可能是 四点中的点.20. 某车间有60名工人,平均每人每天可以加工大齿轮3个或小齿轮4个,已知1个大齿轮和4个小齿轮配为一套,问如何安排工人使生产的产品刚好配套?21. 如图, 是直线 上一点,以 为顶点作 ,且 位于直线 两侧, 平分 . (1)、①当 时,求 的度数;
(1)、①当 时,求 的度数;②当 时,则 的度数为
(2)、通过(1)的计算,请你猜想 和 的数量关系,并说明理由.22. 下表是某网约车公司的专车计价规则.计费项目
起租价
里程费
时长费
远途费
单价
15元
2.5元/公里
1.5元/分
1元/公里
注:车费由起租价、里程费、时长费、远途费四部分构成,其中起租价15元含10分钟时长费和5公里里程费,远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收1元.
(1)、若小李乘坐专车,行车里程为20公里,行车时间为30分,则需付车费元.(2)、若小李乘坐专车,行车里程为 公里,平均时速为 ,则小李应付车费多少元?(用含 的代数式表示)(3)、小李与小王各自乘坐专车,行车车费之和为76元,里程之和为15公里(其中小王的行车里程不超过5公里).如果行驶时间均为 20分钟,那么这两辆专车此次的行驶路程各为多少公里?23. 如图1, 点 在直线 上, ,将. 绕着点 以 的速度逆时针旋转,设旋转时间为 . (1)、如图2,当 平分 时, ;图中 的补角有:;(2)、如图3,当 时, 平分 , 平分 ,求 的度数;(3)、在 绕着点 逆时针旋转的过程中,当 时, .24. 已知 三点在数轴上所对应的数分别为 且 满足 .动点 从点 出发,以2单位/秒的速度向右运动,同时,动点 从点 出发,以1单位秒的速度向左运动,线段 为“变速区”,规则为:从点 运动到点 期间速度变为原来的一半,之后立刻恢复原速,从点 运动到点 期间速度变为原来的两倍,之后也立刻恢复原速.当点 到达点 时,两点都停止运动.设运动的时间为 秒.
(1)、如图2,当 平分 时, ;图中 的补角有:;(2)、如图3,当 时, 平分 , 平分 ,求 的度数;(3)、在 绕着点 逆时针旋转的过程中,当 时, .24. 已知 三点在数轴上所对应的数分别为 且 满足 .动点 从点 出发,以2单位/秒的速度向右运动,同时,动点 从点 出发,以1单位秒的速度向左运动,线段 为“变速区”,规则为:从点 运动到点 期间速度变为原来的一半,之后立刻恢复原速,从点 运动到点 期间速度变为原来的两倍,之后也立刻恢复原速.当点 到达点 时,两点都停止运动.设运动的时间为 秒. (1)、 , , ;(2)、①动点 从点 运动至点 时,求 的值;
(1)、 , , ;(2)、①动点 从点 运动至点 时,求 的值;② 两点相遇时,求相遇点在数轴上所对应的数;
(3)、若点 为线段 中点,当 秒时, .