湖北省武汉市江夏区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、单选题
-
1. 下列方程中,解为 的是( )A、 B、 C、 D、2. 钟表上6时整,钟表的时针和分针构成多少度的角?( )A、180° B、150° C、120° D、90°3. 下列计算正确的是( )A、 B、 C、 D、4. 列等式表示:“ 的2倍与10的和等于18”,下列正确的是( )A、 B、 C、 D、5. 计算: ( )A、-8 B、-7 C、-4 D、-36. 下列各图中,可以是一个正方体的平面展开图的是( )A、
 B、
B、 C、
C、 D、
D、 7. 笔记本的单价是 元,钢笔的单价是 元,甲买3本笔记本和2支钢笔,乙买4本笔记本和3支钢笔,买这些笔记本和钢笔,甲和乙一共花了多少元?( )A、 B、 C、 D、8. 一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件服装仍可获利30元,则这种服装每件的成本是( )A、100元 B、150元 C、200元 D、250元9. 已知 在数轴上的位置如图所示,则 的值是( )
7. 笔记本的单价是 元,钢笔的单价是 元,甲买3本笔记本和2支钢笔,乙买4本笔记本和3支钢笔,买这些笔记本和钢笔,甲和乙一共花了多少元?( )A、 B、 C、 D、8. 一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件服装仍可获利30元,则这种服装每件的成本是( )A、100元 B、150元 C、200元 D、250元9. 已知 在数轴上的位置如图所示,则 的值是( )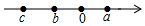 A、 B、 C、 D、10. 如图,点 为线段 上两点, ,且 ,设 ,则方程 的解是( )
A、 B、 C、 D、10. 如图,点 为线段 上两点, ,且 ,设 ,则方程 的解是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
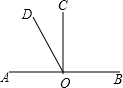
11. 计算: .12. 如图, 是直线 上一点, 是 的平分线, ,则 .
 13. 某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元,则前年的产值是万元14. 已知: ,则 的值为.15. 由 个相同的正方体组成一个立体图形,如图的图形分别是从正面和上面看它得到的平面图形,设 能取到的最大值是 ,则多项式 的值是.
13. 某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元,则前年的产值是万元14. 已知: ,则 的值为.15. 由 个相同的正方体组成一个立体图形,如图的图形分别是从正面和上面看它得到的平面图形,设 能取到的最大值是 ,则多项式 的值是. 16. 一般情况下 不成立,但也有这么一对数可以使得它成立,例如: .我们把能使得 成立的一对数 称为“相伴数对”,记作 .若 是“相伴数对",则 的值为.
16. 一般情况下 不成立,但也有这么一对数可以使得它成立,例如: .我们把能使得 成立的一对数 称为“相伴数对”,记作 .若 是“相伴数对",则 的值为.三、解答题
-
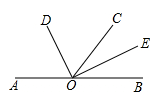
17. 如图,点 在同一条直线上,射线 和射线 分别平分 和 ,若 ,求 及 的度数.
 18. 解下列方程:(1)、(2)、19. 计算:(1)、(2)、20. 化简求值: ,其中 的值是方程 的解, .21. 如图,点 在线段 上, ,线段 的中点 之间的距离是20,求线段 的长.
18. 解下列方程:(1)、(2)、19. 计算:(1)、(2)、20. 化简求值: ,其中 的值是方程 的解, .21. 如图,点 在线段 上, ,线段 的中点 之间的距离是20,求线段 的长.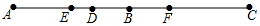 22. 一列火车匀速行驶,经一条长 的隧道需要 的时间隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是 ,假设这列火车的长度为 .(1)、设从车头经过灯到车尾经过灯下火车所走的这段时间内火车的平均速度为 ,从车头进入隧道到车尾离开隧道火车所走的这段时间内火车的平均速度为 ,计算: (结果用含 的式子表示).(2)、求式子: 的值.23. 两点在数轴上的位置如图,点 对应的数值为-5,点 对应的数值为11.(1)、现有两动点 和 ,点 从 点出发以2个单位长度秒的速度向左运动,点 从点 出发以6个单位长度秒的速度同时向右运动,问:运动多长时间满足 ?
22. 一列火车匀速行驶,经一条长 的隧道需要 的时间隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是 ,假设这列火车的长度为 .(1)、设从车头经过灯到车尾经过灯下火车所走的这段时间内火车的平均速度为 ,从车头进入隧道到车尾离开隧道火车所走的这段时间内火车的平均速度为 ,计算: (结果用含 的式子表示).(2)、求式子: 的值.23. 两点在数轴上的位置如图,点 对应的数值为-5,点 对应的数值为11.(1)、现有两动点 和 ,点 从 点出发以2个单位长度秒的速度向左运动,点 从点 出发以6个单位长度秒的速度同时向右运动,问:运动多长时间满足 ? (2)、现有两动点 和 ,点 从 点出发以1个单位长度/秒的速度向右运动,点 从点 出发以5个单位长度/秒的速度同时向左运动,问:运动多长时间满足 ?
(2)、现有两动点 和 ,点 从 点出发以1个单位长度/秒的速度向右运动,点 从点 出发以5个单位长度/秒的速度同时向左运动,问:运动多长时间满足 ? 24. 已知 为直线 上的一点,射线 表示正北方向, ,射线 平分 .
24. 已知 为直线 上的一点,射线 表示正北方向, ,射线 平分 .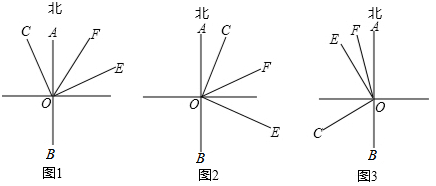 (1)、如图1,若 ,求 的度数.(2)、若将 绕点 旋转至图2的位置,试判断 和 之间的数量关系,并证明你的结果.(3)、若将 绕点 旋转至图3的位置,求满足: 时 的度数.
(1)、如图1,若 ,求 的度数.(2)、若将 绕点 旋转至图2的位置,试判断 和 之间的数量关系,并证明你的结果.(3)、若将 绕点 旋转至图3的位置,求满足: 时 的度数.