辽宁省沈阳市大东区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、单选题
-
1. 下列各数中,为负数的是( )A、4 B、0 C、 D、2. 用一个平面去截一个几何体,截面不可能是圆的几何体的是( )A、
 B、
B、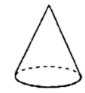 C、
C、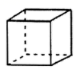 D、
D、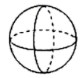 3. 中国的陆地面积和领水面积共约 ,用科学记数法表示 ( )A、 B、 C、 D、4. 下列各式中,正确的是( )A、x2y-2x2y=-x2y B、2a+3b=5ab C、7ab-3ab=4 D、a3+a2=a55. 若 m+n<0,mn>0,那么这两个数( )A、都是正数 B、都是负数 C、一正一负 D、符号不能确定6. 单项式 的系数是( )A、8 B、-8 C、 D、7. 下列调查中,调查方式选择合理的是( )A、为了了解新型炮弹的杀伤半径,选择全面调查 B、为了了解某种灯泡的使用寿命,选择抽样调查 C、为了了解神舟飞船的设备零件的质量情况,选择抽样调查 D、为了了解一批袋装食品是否含有防腐剂,选择全面调查8. 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
3. 中国的陆地面积和领水面积共约 ,用科学记数法表示 ( )A、 B、 C、 D、4. 下列各式中,正确的是( )A、x2y-2x2y=-x2y B、2a+3b=5ab C、7ab-3ab=4 D、a3+a2=a55. 若 m+n<0,mn>0,那么这两个数( )A、都是正数 B、都是负数 C、一正一负 D、符号不能确定6. 单项式 的系数是( )A、8 B、-8 C、 D、7. 下列调查中,调查方式选择合理的是( )A、为了了解新型炮弹的杀伤半径,选择全面调查 B、为了了解某种灯泡的使用寿命,选择抽样调查 C、为了了解神舟飞船的设备零件的质量情况,选择抽样调查 D、为了了解一批袋装食品是否含有防腐剂,选择全面调查8. 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )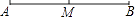 A、BM= AB B、AM+BM=AB C、AM=BM D、AB=2AM9. 下列方程中,解为x=2的方程是( )A、3x+3=x B、-x+3=0 C、2x=6 D、5x-2=810. 如图所示,点 在点 的北偏东60°, ,则射线 的方向是( )
A、BM= AB B、AM+BM=AB C、AM=BM D、AB=2AM9. 下列方程中,解为x=2的方程是( )A、3x+3=x B、-x+3=0 C、2x=6 D、5x-2=810. 如图所示,点 在点 的北偏东60°, ,则射线 的方向是( ) A、北偏西50° B、西偏北50° C、北偏西40° D、北偏西30°
A、北偏西50° B、西偏北50° C、北偏西40° D、北偏西30°二、填空题
-
11. 的相反数是 , 小于 的最大整数是.12. 在数轴上把表示-3的对应点沿数轴移动5个单位后,所得的对应点表示的数是.13. 已知 ,则 的值是.14. 一件风衣,按进价提高50%后标价,后因季节关系按标价的八折出售,每件卖240元,这件风衣的进价是元.15. 如图,将长方形纸片进行折叠, , 为折痕, 与 , 与 , 与C′重合,若 则 的度数为.
 16. 如图,图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第n个图形中菱形的个数为
16. 如图,图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第n个图形中菱形的个数为
三、解答题
-
17. 计算:(1)、 ;(2)、 ;(3)、 .18. 解方程:(1)、 ;(2)、19. 先化简,再求值:
,其中 , .
20. 由十个小立方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小立方体的个数,请在网格中画出从正面和左面看到的几何体的形状图.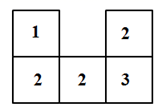

 21. 某区为响应市政府号召,在所有中学开展“创文创卫”活动.在活动中设置了“A.文明礼仪;B.环境保护;C.卫生保洁;D.垃圾分类”四个主题,每个学生选一个主题参与.为了解活动开展的情况,在全区随机抽取部分中学生进行调查,并根据调查结果绘制成了如下条形统计图和扇形统计图:
21. 某区为响应市政府号召,在所有中学开展“创文创卫”活动.在活动中设置了“A.文明礼仪;B.环境保护;C.卫生保洁;D.垃圾分类”四个主题,每个学生选一个主题参与.为了解活动开展的情况,在全区随机抽取部分中学生进行调查,并根据调查结果绘制成了如下条形统计图和扇形统计图: (1)、此次调查的学生人数是人,条形统计图中 , ;(2)、请根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中“选项D.垃圾分类”对应扇形的圆心角的大小为度;(4)、依据本次调查的结果,估计全区12000名中学生选“A.文明礼仪”约有多少人?22. 一项工程,甲队单独完成需40天,乙队单独完成需50天,现甲队单独做4天后两队合作.(1)、求甲、乙合作多少天才能把该工程完成.(2)、在(1)的条件下,甲队每天的施工费用为2500元,乙队每天的施工费用为3000元,求完成此项工程需付给甲、乙两队共多少元.23. 在 和 中,
(1)、此次调查的学生人数是人,条形统计图中 , ;(2)、请根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中“选项D.垃圾分类”对应扇形的圆心角的大小为度;(4)、依据本次调查的结果,估计全区12000名中学生选“A.文明礼仪”约有多少人?22. 一项工程,甲队单独完成需40天,乙队单独完成需50天,现甲队单独做4天后两队合作.(1)、求甲、乙合作多少天才能把该工程完成.(2)、在(1)的条件下,甲队每天的施工费用为2500元,乙队每天的施工费用为3000元,求完成此项工程需付给甲、乙两队共多少元.23. 在 和 中, (1)、如图1,已知 ,当 时,求 的度数:(2)、如图2,已知 , ,且 时,请直接写出∠BOD的度数;(3)、如图3,当 , ,且 时,请直接用含有 , , 的代数式表示 的值24. 阅读材料:求 的值.
(1)、如图1,已知 ,当 时,求 的度数:(2)、如图2,已知 , ,且 时,请直接写出∠BOD的度数;(3)、如图3,当 , ,且 时,请直接用含有 , , 的代数式表示 的值24. 阅读材料:求 的值.解:设 ①,将等式①的两边同乘以2,
得 ②,
用②-①得,
即 .
即 .
请仿照此法计算:
(1)、请直接填写 的值为;(2)、求 值;(3)、请直接写出 的值.25. 如图,在长方形 中, , .动点 从 出发,每秒1个单位长度的速度沿 匀速运动,到 点停止运动;同时点 从 点出发,以每秒2个单位长度的速度沿 匀速运动,到 点停止运动.设 点运动的时间为 秒 . (1)、点 在 上运动时, , , 点 在 上运动时, , (用含 的代数式表示);(2)、求当 为何值时, ;(3)、当 , 两点在运动路线上相距3个单位长度时,请直接写出 的值.
(1)、点 在 上运动时, , , 点 在 上运动时, , (用含 的代数式表示);(2)、求当 为何值时, ;(3)、当 , 两点在运动路线上相距3个单位长度时,请直接写出 的值.