甘肃省天水市麦积区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、单选题

1. $- 3$ 的绝对值是（　　　）

A、3 B、 $- 3$ C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列各式的值最小的是（）

A、 $1 - 3$ B、 $- 2 {}^{2}$ C、 $- 4 \times 0$ D、 $| - 5 |$

查看试题解析
3. 下列说法中正确的是（）

A、 $\frac{π}{2}$ 不是单项式 B、 $- 2^{3} x y$ 的系数是-2，次数是5 C、 $- 3 a b^{2}$ 和 $b^{2} a$ 是同类项 D、多项式 $- x^{7} y + 4 x^{5} - 2$ 的次数是7，项数是3

查看试题解析
4. 已知x－2y－4＝－1，则代数式3－2x＋4y的值为（）

A、－7 B、－3 C、0 D、9

查看试题解析
5. 如图是一个正方体的表面展开图，则原正方体中与“我”字所在的面相对的面上标的字是（）.

A、我 B、的 C、梦 D、国

查看试题解析
6. 以下说法正确的是（）

A、两点之间直线最短 B、延长直线 $A B$ 到点 $E$ ，使 $B E = A B$ C、相等的角是对顶角 D、连结两点的线段的长度就是这两点间的距离

查看试题解析
7. 点E在线段CD上，下面四个等式①CE=DE；②DE= $\frac{1}{2}$ CD；③CD=2CE；④CD= $\frac{1}{2}$ DE．其中能表示E是线段CD中点的有（）

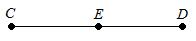A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 甲、乙两个城市，乙城市位于甲城市北偏东50°方向，距离为80km，那么甲城市位于乙城市（）

A、南偏东50°方向，距离为80km B、南偏西50°方向，距离为80km C、南偏东40°方向，距离为80km D、南偏西40°方向，距离为80km

查看试题解析
9. 如图，给出下列条件：①∠1＝∠2：②∠3＝∠4：③AB∥CE，且∠ADC＝∠B：④AB∥CE，且∠BCD＝∠BAD.其中能推出BC∥AD的条件为（）

A、①② B、②④ C、②③ D、②③④

查看试题解析
10. 如图，已知∠1＝∠2，∠3＝∠4，∠BOD＝ $\frac{1}{2}$ ∠AOB＝90°．下列判断：①射线OF是∠BOE的角平分线；②∠DOE的补角是∠BOC；③∠AOC的余角只有∠COD；④∠DOE的余角有∠BOE和∠COD；⑤∠COD＝∠BOE．其中正确的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 若a，b互为倒数，则 $- 2 a b$ 的值为.

查看试题解析
12. 若 $- m^{2} n^{y}$ 与 $m^{x} n^{}$ 是同类项，则 $x + y =$ .

查看试题解析
13. 一个多项式加上 $2 x^{2} - 4 x - 3$ 得 $- x^{2} + 3 x$ ，则这个多项式为.

查看试题解析
14. 如图，点B是线段AC上一点，点O是线段AC的中点，且AB＝20，BC＝8.则线段OB的长为.

查看试题解析
15. 如图，AB∥CD，CE∥GF，若∠1＝60°，则∠2＝°.

查看试题解析
16. 若 ${(2 x + 1)}^{2} + | y - 2 | = 0$ ，则 $x^{y} =$ .

查看试题解析
17. 将多项式 $5 x^{2} y + y^{3} - 3 x y^{2} - x^{3}$ 按 $x$ 降幂排列为.

查看试题解析
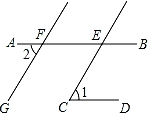18. 下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形.仔细观察图形可知：

第1个图形中有1块黑色的瓷砖，可表示为 $1 = \frac{(1 + 1) \times 1}{2}$ ；

第2个图形中有3块黑色的瓷砖，可表示为 $1 + 2 = \frac{(1 + 2) \times 2}{2}$ ；

第3个图形中有6块黑色的瓷砖，可表示为 $1 + 2 + 3 = \frac{(1 + 3) \times 3}{2}$ ；

则第 $n$ 个图形中有块黑色的瓷砖（ $n$ 为正整数）.

查看试题解析

三、解答题

19. 计算和化简

(1)、计算：24÷[（﹣2）³+4]﹣3×（﹣11）

(2)、化简：2（x²-x+1）-（-2x+3x²）+（1-x）

查看试题解析
20. 化简求值：已知 $A = - a^{2} + 2 a b + 2 b^{2}$ ， $B = 2 a^{2} - 2 a b - b^{2}$ ，当 $a = - \frac{1}{2}$ ， $b = 1$ 时，求 $2 A + B$ 的值．

查看试题解析
21. 有若干个完全相同的小正方体堆成的一个几何体，如图所示.请在方格纸上画出它的三视图.

查看试题解析
22. 一个角的补角加上10°后，等于这个角的余角的3倍，求这个角的余角和补角的度数.

查看试题解析
23. 如图，C是线段AB上一点，M是AC的中点，N是BC的中点

(1)、若AM=1，BC=4，求MN的长度.

(2)、若 AB=6，求 MN 的长度.

查看试题解析
24. 如图，EF//AD，∠1＝∠2，∠BAC＝82°，请将求∠AGD的过程填写完整.

解：因为EF//AD

所以∠2＝∠_▲_（_▲_）

又因为∠1＝∠2

所以∠1＝∠3（_▲_）

所以AB//_▲_（_▲_）

所以∠BAC+∠_▲_＝180°（_▲__）

因为∠BAC＝82°

所以∠AGD＝_▲_°

查看试题解析
25. 如图，射线 $O C$ 、 $O D$ 在 $∠ A O B$ 的内部.

(1)、 $∠ A O B = 169 °$ ， $∠ A O C = ∠ B O D = 90 °$ ，求 $∠ C O D$ 的度数.

(2)、当 $∠ A O C = ∠ B O D = 90 °$ ，试判断 $∠ A O D$ 与 $∠ B O C$ 的关系，说明理由.

(3)、当 $∠ A O C = ∠ B O D = α$ ，（2）中的结论还存在吗？为什么？

查看试题解析