浙江省杭州市余杭区三校2021届九年级上学期数学期末联考试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分）

1. 若2a＝5b ，则 $\frac{a - b}{a + b}$ 的值为（）

A、 $- \frac{3}{7}$ B、 $\frac{3}{7}$ C、 $\frac{3}{5}$ D、 $\frac{7}{3}$

查看试题解析
2. 两道单选题都含有A、B、C、D四个选项，小明同学在不会做的情况下，两题都答对的概率是(　　)

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{16}$ D、 $\frac{3}{8}$

查看试题解析
3. 关于二次函数y=2x²+x-1，下列说法正确的是（）

A、图象与y轴的交点坐标为(0，1) B、图象的对称轴在y轴的右侧 C、当x＜0时，y的值随x值的增大而减小 D、y的最小值为- $\frac{9}{8}$

查看试题解析
4. 如图，在⊙O中，AB是弦，OC⊥AB，垂足为C，若AB＝16，OC＝6，则⊙O的半径OA等于（）

A、16 B、12 C、10 D、8

查看试题解析
5. 如图，一个梯子靠在垂直水平地面的墙上，梯子AB的长是2米．若梯子与地面的夹角为 $α$ ，则梯子顶端到地面的距离（BC的长）为（）

A、 $2 \sin α$ 米 B、 $2 \cos α$ 米 C、 $\frac{2}{\sin α}$ 米 D、 $\frac{2}{\cos α}$ 米

查看试题解析
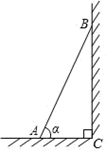6. 如图，在Rt△ABC中，∠ACB＝90°，AC＝24，AB＝25，CD是斜边AB上的高，则cos∠BCD的值为（）

A、 $\frac{7}{25}$ B、 $\frac{24}{25}$ C、 $\frac{7}{24}$ D、 $\frac{24}{7}$

查看试题解析
7. 如图， $A B$ 为⊙ $O$ 的切线， $A$ 为切点， $O B$ 交⊙ $O$ 于点 $D$ ， $C$ 为⊙ $O$ 上一点，若 $∠ A B O = 42 °$ ，则 $∠ A C D$ 的度数为（）

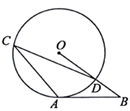A、48° B、24° C、36° D、72°

查看试题解析
8. 如图，身高1.5米的小西站在点D处，此时路灯M照射的影子AD为2.5米，小西沿着 $A \to B$ 的方向行走4.5米至点F，此时影子 $N F$ 为1米，则路灯BM的高度为（）

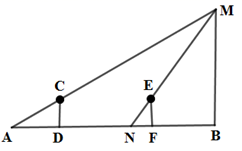A、3米 B、3.5米 C、4.5米 D、6米

查看试题解析
9. 如图，边长为1的菱形ABCD绕点A旋转，当B、C两点恰好落在扇形AEF的弧EF上时，弧BC的长度等于（）

A、 $\frac{π}{6}$ B、 $\frac{π}{5}$ C、 $\frac{π}{4}$ D、 $\frac{π}{3}$

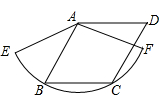查看试题解析
10. 二次函数y＝ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为(1，﹣4a)，点A(4，y₁)是该抛物线上一点，若点D(x₂ ， y₂)是抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②若y₂＞y₁ ，则x₂＞4；③若0≤x₂≤4，则0≤y₂≤5a；④若方程a(x+1)(x﹣3)＝﹣1有两个实数根x₁和x₂ ，且x₁＜x₂ ，则﹣1＜x₁＜x₂＜3．其中正确结论的个数是（）

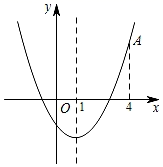A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 如图，线段CD两个端点的坐标分别为C（4，4），D（6，2），以原点O为位似中心，在第一象限内将线段CD缩小为原来的一半后得到线段AB，则端点A的坐标为.

查看试题解析
12. 如图，在△ABC中，∠A＝30°，tanB＝ $\frac{\sqrt{3}}{2}$ ，AC＝2 $\sqrt{3}$ ，AB的长．

查看试题解析
13. 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同.若从中随机摸出一个球，它是白球的概率为 $\frac{2}{5}$ ，则n=.

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = 4 \sqrt{3} ， B C = 4 ， ∠ A B C = 90^{\circ}$ ，以 $A B$ 为直径画弧，与 $A C$ 交于点D，则图中阴影部分的面积为（结果保留 $π$ ）.

查看试题解析
15. 如图，在矩形 ABCD 中，AB=2，BC=4，⊙D 的半径为 1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为 .

查看试题解析
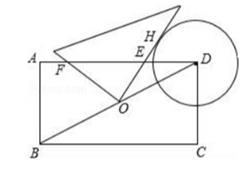16. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE ，使点B落在点F处，连接AF ，则当线段AF的长取最小值时，sin∠FBD是．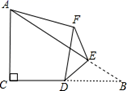

查看试题解析

三、解答题（本大题共7小题，共66.0分）

17. 某校举行秋季运动会，甲、乙两人都报名参加100m短跑比赛，预赛分A、B、C三组进行，运动员通过抽签决定分组.

(1)、甲分到A组的概率为；

(2)、利用树状图或列表的方法求甲、乙两人不在同一组的概率.

查看试题解析
18. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ，垂足为D， $B C = 12 ， A D = 6 ， \tan C = \frac{3}{2}$ .

(1)、求 $\sin ∠ A B D$ 的值；

(2)、过点B作 $B E ⊥ B C$ ，若 $B E = 10$ ，求 $A E$ 的长.

查看试题解析
19. 如图，在 $△ A B C$ 中，点D、E分别在边AB、AC上， $∠ A E D = ∠ B$ ， AG分别交线段DE、BC于点F、G ，且AD： $A C = D F$ ： $C G .$ 求证：

(1)、AG平分 $∠ B A C$ ；

(2)、EF·CG=DF·BG ．

查看试题解析
20. 如图1，AC⊥CH于点C ，点B是射线CH上一动点，将△ABC绕点A逆时针旋转60°得到△ADE（点D对应点C）．

(1)、延长ED交CH于点F ，求证：FA平分∠CFE；

(2)、如图2，当∠CAB＞60°时，点M为AB的中点，连接DM ，请判断DM与DA、DE的数量关系，并证明．

查看试题解析
21. 在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行
销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y(个)于销售单价x(元/个)之间的对应关系如图所示．

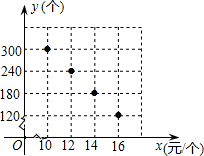(1)、试判断y与x之间的函数关系，并求出函数关系式；

(2)、若许愿瓶的进价为6元/个，按照上述市场调查销售规律，求利润w(元)与销售单价x(元/个)之间的
函数关系式；

(3)、若许愿瓶的进货成本不超过900元，要想获得最大利润，试求此时这种许愿瓶的销售单价，并求出
最大利润

查看试题解析
22. 如图，抛物线 $y = a x^{2} - \frac{3}{2} x + c (a \neq 0)$ 与x轴交于点A，B，与y轴交于点 $C (0 ， - 2)$ ， $\tan ∠ A B C = \frac{1}{2}$ .直线 $x = 1$ 交 $B C$ 于点D，点P是直线 $B C$ 下方抛物线上一动点，连接PD.

(1)、求此抛物线的解析式；

(2)、如图1，连接 $P C$ ，求 $△ P C D$ 面积的最大值及此时点P的坐标；

(3)、如图2，连接 $A C$ ，过点P作 $P E ⊥ B C$ 于点E，是否存在点P使以P，D，E三点为顶点的三角形与 $△ A B C$ 相似，若存在，直接写出点P的坐标；若不存在，请说明理由.

查看试题解析
23. 如图，△ABC内接于⊙O，AD平分∠BAC交BC边于点E，交⊙O于点D，过点A作AF⊥BC于点F，设⊙O的半径为R，AF＝h．

(1)、过点D作直线MN∥BC，求证：MN是⊙O的切线；

(2)、求证：AB•AC＝2R•h；

(3)、设∠BAC＝2α，求 $\frac{A B + A C}{A D}$ 的值（用含α的代数式表示）．

查看试题解析