陕西省渭南市韩城市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、选择题(共10小题).
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算:sin60°•tan30°=( )A、1 B、 C、 D、23. 将一个圆柱和一个正三棱柱如图放置,则所构成的几何体的主视图是( )
2. 计算:sin60°•tan30°=( )A、1 B、 C、 D、23. 将一个圆柱和一个正三棱柱如图放置,则所构成的几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A'BC’,连接A'C,则A'C的长为( )
4. 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A'BC’,连接A'C,则A'C的长为( ) A、6 B、4+2 C、4+3 D、2+35. 用扇形统计图反应地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( )
A、6 B、4+2 C、4+3 D、2+35. 用扇形统计图反应地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( ) A、0.2 B、0.3 C、0.4 D、0.56. 若关于x的一元二次方程x2﹣2x+m=0有实数根,则实数m的取值范围是( )A、m<1 B、m≤1 C、m>1 D、m≥17. 如图,正比例函数y=x与反比例函数y= 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于y= 的函数值时,x的取值范围是( )
A、0.2 B、0.3 C、0.4 D、0.56. 若关于x的一元二次方程x2﹣2x+m=0有实数根,则实数m的取值范围是( )A、m<1 B、m≤1 C、m>1 D、m≥17. 如图,正比例函数y=x与反比例函数y= 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于y= 的函数值时,x的取值范围是( )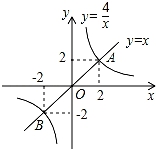 A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>28. 如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对( )
A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>28. 如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对( ) A、6对 B、5对 C、4对 D、3对9. 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
A、6对 B、5对 C、4对 D、3对9. 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )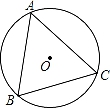 A、4 B、6 C、2 D、810. 已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
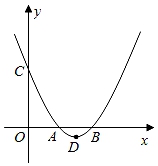
A、4 B、6 C、2 D、810. 已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③4a﹣2b+c>0;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(共4小题,每小题3分,计12分)
-
11. 若点M(3,a﹣2),N(b,a)关于原点对称,则a+b= .12. 已知在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .13. 将二次函数y=x2﹣4x+a的图象向左平移1个单位,再向上平移1个单位,若得到的函数图象与直线y=2有两个交点,则a的取值范围是.14. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE+FH的最大值为.

三、解答题(共11小题,计78分.解答应写出过程)
-
15. 解方程:(x﹣3)(x﹣2)﹣4=0.16. 如图,已知△ABC,请用尺规作△ABC的外接圆⊙O.(保留作图痕迹,不写作法)
 17. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
17. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上. (1)、请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.18. 为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均20平方米提高到24.2平方米,求城镇居民住房面积的年平均增长率.19. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)、请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.18. 为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均20平方米提高到24.2平方米,求城镇居民住房面积的年平均增长率.19. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA= (1)、求BD的长;(2)、求tanC的值.20. 如图,在锐角△ABC中,AB=4,BC=5,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 , 连接AA1 , CC1 , 若△ABA1的面积为4,求△CBC1的面积.
(1)、求BD的长;(2)、求tanC的值.20. 如图,在锐角△ABC中,AB=4,BC=5,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 , 连接AA1 , CC1 , 若△ABA1的面积为4,求△CBC1的面积. 21. 如图,平行四边形OABC的顶点O在原点上,顶点A,C分别在反比例函数y= (k≠0,x>0),y=﹣ (x<0)的图象上,对角线AC⊥y轴于D,已知点D的坐标为D(0,5).
21. 如图,平行四边形OABC的顶点O在原点上,顶点A,C分别在反比例函数y= (k≠0,x>0),y=﹣ (x<0)的图象上,对角线AC⊥y轴于D,已知点D的坐标为D(0,5).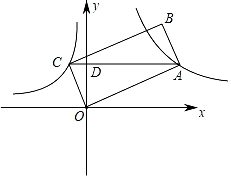 (1)、求点C的坐标;(2)、若平行四边形OABC的面积是55,求k的值.22. 全运会吉祥物以陕西秦岭独有的四个国宝级动物“金丝猴、羚牛、大熊猫、朱鹮”为创意原型,设计了一组幸福快乐、充满活力、精神焕发、积极向上的运动吉祥物形象.现有四张纪念卡片分别绘有吉祥物的图案(如图),纪念卡背面完全相同.
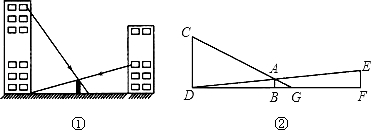
(1)、求点C的坐标;(2)、若平行四边形OABC的面积是55,求k的值.22. 全运会吉祥物以陕西秦岭独有的四个国宝级动物“金丝猴、羚牛、大熊猫、朱鹮”为创意原型,设计了一组幸福快乐、充满活力、精神焕发、积极向上的运动吉祥物形象.现有四张纪念卡片分别绘有吉祥物的图案(如图),纪念卡背面完全相同. (1)、小丽从四张纪念卡任意抽取一张,则小丽抽取到的卡片绘有吉祥物“羚羚”的概率为;(2)、小明先从中随机抽取一张卡片,记录下卡片上的动物名称,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的动物名称.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是“熊熊”的概率.23. 如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示.根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高8米,DF=120米,tan∠AGB= ,求甲、乙两人的观测点到地面的距离的差.
(1)、小丽从四张纪念卡任意抽取一张,则小丽抽取到的卡片绘有吉祥物“羚羚”的概率为;(2)、小明先从中随机抽取一张卡片,记录下卡片上的动物名称,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的动物名称.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是“熊熊”的概率.23. 如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示.根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高8米,DF=120米,tan∠AGB= ,求甲、乙两人的观测点到地面的距离的差.