辽宁省沈阳市沈河区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、选择题(共10小题).
-
1. 若 = ,则 的值为( )A、 B、 C、 D、2. 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
 A、
A、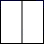 B、
B、 C、
C、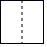 D、
D、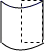 3. 矩形具有而菱形不具有的性质是( )
3. 矩形具有而菱形不具有的性质是( )
A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等4. 在利用正六面体骰子进行频率估计概率的实验中,小颖同学统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( ) A、朝上的点数是 5 的概率 B、朝上的点数是奇数的概率 C、朝上的点数是大于 2 的概率 D、朝上的点数是 3 的倍数的概率5. 下列一元二次方程没有实数根的是( )A、x2+x+1=0 B、x2+x﹣1=0 C、x2﹣2x﹣1=0 D、x2﹣2x+1=06. 已知反比例函数y=﹣ ,下列说法中正确的是( )A、该函数的图象分布在第一、三象限 B、点(2,3)在该函数图象上 C、y随x的增大而增大 D、该图象关于原点成中心对称7. 在平面直角坐标系中,点A,B的坐标分别是(4,2),B(5,0),以O为位似中心,相似比为 ,把△ABO缩小,得到△A1B1O,则点A的对应点A1的坐标为( )A、(2,1) B、(2,﹣1) C、(﹣2,﹣1) D、(2,1)或(﹣2,﹣1)8. 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+ =0的根的情况是( )
A、朝上的点数是 5 的概率 B、朝上的点数是奇数的概率 C、朝上的点数是大于 2 的概率 D、朝上的点数是 3 的倍数的概率5. 下列一元二次方程没有实数根的是( )A、x2+x+1=0 B、x2+x﹣1=0 C、x2﹣2x﹣1=0 D、x2﹣2x+1=06. 已知反比例函数y=﹣ ,下列说法中正确的是( )A、该函数的图象分布在第一、三象限 B、点(2,3)在该函数图象上 C、y随x的增大而增大 D、该图象关于原点成中心对称7. 在平面直角坐标系中,点A,B的坐标分别是(4,2),B(5,0),以O为位似中心,相似比为 ,把△ABO缩小,得到△A1B1O,则点A的对应点A1的坐标为( )A、(2,1) B、(2,﹣1) C、(﹣2,﹣1) D、(2,1)或(﹣2,﹣1)8. 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+ =0的根的情况是( ) A、无实数根 B、有两个相等实数根 C、有两个异号实数根 D、有两个同号不等实数根9. 如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2 , 周长分别是C1与C2 , 则下列说法正确的是( )
A、无实数根 B、有两个相等实数根 C、有两个异号实数根 D、有两个同号不等实数根9. 如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2 , 周长分别是C1与C2 , 则下列说法正确的是( ) A、 = B、 = C、 = D、 =10. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x= ,且经过点(2,0),下列说法:①abc>0;②b2﹣4ac>0;③x=﹣1是关于x的方程ax2+bx+c=0的一个根;④a+b=0.其中正确的个数为( )
A、 = B、 = C、 = D、 =10. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x= ,且经过点(2,0),下列说法:①abc>0;②b2﹣4ac>0;③x=﹣1是关于x的方程ax2+bx+c=0的一个根;④a+b=0.其中正确的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(共6小题).
-
11. 方程x(x+3)=0的解是 .12. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为m.
 13. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是.14. 如图,公路AC与BC互相垂直,垂足为点C,公路AB的中点M与点C被湖隔开,若测得AB的长为4.6km,则点M与C之间的距离是km.
13. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是.14. 如图,公路AC与BC互相垂直,垂足为点C,公路AB的中点M与点C被湖隔开,若测得AB的长为4.6km,则点M与C之间的距离是km. 15. 若关于x的一元二次方程(m﹣3)x2+6x+m2﹣7m+12=0有一个根是0,那么m的值为.16. 如图,在四边形ABCD中,AD= AB,∠A=30°,将线段CD绕点C逆时针旋转90°,并延长至其 倍(即CE= CD),过点E作EF⊥AB于点F,当AD=6 ,BF=3,EF= 时,边BC的长是.
15. 若关于x的一元二次方程(m﹣3)x2+6x+m2﹣7m+12=0有一个根是0,那么m的值为.16. 如图,在四边形ABCD中,AD= AB,∠A=30°,将线段CD绕点C逆时针旋转90°,并延长至其 倍(即CE= CD),过点E作EF⊥AB于点F,当AD=6 ,BF=3,EF= 时,边BC的长是.
三、解答题(第17小题6分,第18,19小题各8分,共22分)
-
17. 计算:4sin260°+ cos45°﹣2tan60°•tan30°.18. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
 (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)19. 如图,在正方形ABCD中,对角线BD所在的直线上有两点E,F(点E,F在正方形ABCD的外部),满足BE=DF,连接AE,AF,CE,CF.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)19. 如图,在正方形ABCD中,对角线BD所在的直线上有两点E,F(点E,F在正方形ABCD的外部),满足BE=DF,连接AE,AF,CE,CF. (1)、求证:四边形AECF是菱形;(2)、若AB=4,sin∠AFE= ,则四边形AECF的面积是.
(1)、求证:四边形AECF是菱形;(2)、若AB=4,sin∠AFE= ,则四边形AECF的面积是.四、(每小题8分,共16分)
-
20. 某地区2018年投入教育经费2000万元,2020年投入教育经费2880万元.(1)、求2018年至2020年该地区投入教育经费的年平均增长率;(2)、根据(1)所得的年平均增长率,预计2021年该地区将投入教育经费多少万元.21. 如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)

五、(本题10分)
-
22. 如图,平行于y轴的直尺(一部分)与双曲线y= (x>0)交于点A和C,与x轴交于点B和D,点A和B的刻度分别为5cm和2cm,直尺的宽度为2cm,OB=2cm.(注:平面直角坐标系内一个单位长度为1cm)
 (1)、点A的坐标为;(2)、求双曲线y= 的解析式;(3)、若经过A,C两点的直线解析式为y=mx+b,请直接写出关于x的不等式mx+b- <0的解集.
(1)、点A的坐标为;(2)、求双曲线y= 的解析式;(3)、若经过A,C两点的直线解析式为y=mx+b,请直接写出关于x的不等式mx+b- <0的解集.六、(本题10分)
-
23. 某厂为满足市场需求,改造了10条口罩生产线,每条生产线每天可生产口罩500个,如果每增加一条生产线,每条生产线每天就会少生产20个口罩,设增加x条生产线(x为正整数),每条生产线每天可生产口罩y个.(1)、请直接写出y与x之间的函数关系式和自变量取值范围;(2)、设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出当x为多少时,每天生产的口罩数量w最多?最多为多少个?(3)、由于口罩供不应求,所以每天生产的口罩数量不能低于6000个,请直接写出需要增加的生产线x条的取值范围.
七、(本题12分)
-
24. 在矩形ABCD中,AD=6,AB=2 ,点E是边AD上的一个动点,连接BE,以BE为一边在其左上方作矩形BEFG,过点F作直线AD的垂线,垂足为点H,连接DF.
 (1)、当BE=EF时.
(1)、当BE=EF时.①求证:FH=AE;
②当△DEF的面积是 时,求线段DE的长;
(2)、如图2,当BE= EF,且射线FE经过CD的中点时,请直接写出线段FH长.八、(本题12分)
-
25. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是第一象限内抛物线上的动点.
 (1)、求抛物线的解析式;(2)、连接BC与OP,交于点D,求当 的值最大时点P的坐标;(3)、点F与点C关于抛物线的对称轴成轴对称,当点P的纵坐标为2时,过点P作直线PQ∥x轴,点M为直线PQ上的一个动点,过点M作MN⊥x轴于点N,在线段ON上任取一点K,当有且只有一个点K满足∠FKM=135°时,请直接写出此时线段ON的长.
(1)、求抛物线的解析式;(2)、连接BC与OP,交于点D,求当 的值最大时点P的坐标;(3)、点F与点C关于抛物线的对称轴成轴对称,当点P的纵坐标为2时,过点P作直线PQ∥x轴,点M为直线PQ上的一个动点,过点M作MN⊥x轴于点N,在线段ON上任取一点K,当有且只有一个点K满足∠FKM=135°时,请直接写出此时线段ON的长.
-
-
-