辽宁省大连市甘井子区2021届九年级上学期数学期末考试试卷
试卷更新日期：2021-02-03 类型：期末考试
一、选择题（共10小题）.
-
1. 下列图形中，不是中心对称图形的是（ ）A、
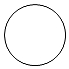圆
B、
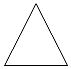等边三角形
C、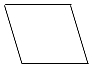
平行四边形
D、
正方形
2. 下列事件中，属于必然事件的是（ ）A、明天的最高气温将达35℃ B、任意购买一张动车票，座位刚好挨着窗口 C、掷两次质地均匀的骰子，其中有一次正面朝上 D、对顶角相等3. 抛物线y＝3x2向左平移4个单位，再向下平移2个单位，所得到的抛物线是（ ）A、y＝3（x﹣4）2+2 B、y＝3（x﹣4）2﹣2 C、y＝3（x+4）2﹣2 D、y＝3（x+4）2+24. 已知点P的坐标是（﹣6，5），则P点关于原点的对称点的坐标是（ ）A、（﹣6，﹣5） B、（6，5） C、（6，﹣5） D、（5，﹣6）5. 关于x的方程x2﹣4x+m＝0有一个根为﹣1，则另一个根为（ ）A、﹣2 B、2 C、﹣5 D、56. 如图，四边形ABCD内接于⊙O，若∠A＝110°，则∠C的度数为（ ）
A、70° B、100° C、110° D、120°7. 如图，四边形ABCD∽四边形EFGH，∠A＝80°，∠C＝90°，∠F＝70°，则∠E的度数为（ ）
A、70° B、80° C、90° D、120°8. 在一个不透明的盒子里装有200个红、黄两种颜色的小球，这些球除颜色外其他完全相同，每次摸球前先将盒子里的球摇匀，任意摸出一个球，记下颜色后再放回盒子，通过大量重复试验后发现，摸到黄球的频率稳定在45%，那么估计盒子中黄球的个数为（ ）A、80 B、90 C、100 D、1109. 在Rt△ABC中，∠B＝90°，AB＝4，BC＝3，则tanA的值为（ ）
A、 B、 C、 D、10. 公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m2 ， 求原正方形空地的边长.设原正方形的空地的边长为xm，则可列方程为（ ）
A、（x+1）（x+2）＝18 B、x2﹣3x+16＝0 C、（x﹣1）（x﹣2）＝18 D、x2+3x+16＝0二、填空题（共6小题）.
-
11. cos60°＝ ．12. 若关于x的一元二次方程x2﹣2x+m＝0有两个相等的实数根，则实数m的值为.13. 如图，在平面直角坐标系中，正方形OABC与正方形ODEF是位似图形，点O为位似中心，位似比为2：3，点B、E在第一象限，若点A的坐标为（4，0），则点E的坐标是 ．
14. 如图，在平面直角坐标系中，△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心，旋转得到△A′B′C′，则旋转中心的坐标是.
15. 如图，若被击打的小球飞行高度h（单位：m）与飞行时间t（单位：s）之间具有的关系为h＝20t﹣5t2 ， 则小球从飞出到落地所用的时间为s.
16. 已知一个圆锥的底面半径长为3cm、母线长为6cm，则圆锥的侧面积是cm2.三、解答题（本题共4小题，其中17、18、19题各9分，20题12分，共39分）
-
17. 按要求解方程：(1)、x2﹣x﹣2＝0（公式法）；(2)、2x2+2x﹣1＝0（配方法）.18. 一个不透明的口袋中装有 个红球和 个白球，小球除颜色外其余均相同．从口袋中随机摸出一个小球，记下颜色后放回，再随机摸出一个小球．请用画树状图(或列表) 的方法，求两次摸出的小球颜色不同的概率．19. 如图，在矩形ABCD中，已知AD＞AB.在边AD上取点E，连结CE.过点E作EF⊥CE，与边AB的延长线交于点F.
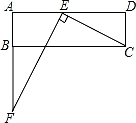(1)、求证：△AEF∽△DCE.(2)、若AB＝3，AE＝4，DE＝6，求线段BF的长.20. 如图，在平面直角坐标系xOy中，二次函数y＝x2+bx+c的图象与x轴，y轴的交点分别为（1，0）和（0，﹣3）.
(1)、求此二次函数的表达式；(2)、结合函数图象，直接写出当y＞﹣3时，x的取值范围.四、解答题（本题共3小题，其中21题9分22、23题各10分，共29分
-
21. 据统计，某市2018年某种品牌汽车的年产量为64万辆，到2020年，该品牌汽车的年产量达到100万辆.若该品牌汽车年产量的年平均增长率从2018年开始五年内保持不变.(1)、求年平均增长率；(2)、求该品牌汽车2021年的年产量为多少万辆？22. 如图，甲、乙两栋大楼相距78米，一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米，求乙楼的高度是多少米？（结果精确到0.1米）
【参考数据：sin27°＝0.45，cos27°＝0.89，tan27°＝0.51】
23. 如图，AB是⊙O的直径，点C在⊙O上，∠CAB的平分线交⊙O于点D，过点D作AC的垂线交AC的延长线于点E.
(1)、证明：ED是⊙O的切线；(2)、若⊙O半径为3，CE＝2，求BC的长.五、解答题（本题共3小题，其中24、25题各11分，26题12分，共34分）
-
24. 如图，在Rt△ABC中，∠ACB＝90°，BC＝6，sin∠A＝ .点D从点A出发，以每秒1个单位长度的速度沿AC向终点C运动，同时点E从点B出发，以相同速度沿BA方向运动，过点E作EF⊥AB，过点D作DF⊥EF垂足为F，连结ED，当点D运动到终点时，点E也停止运动.设△EDF与△ABC重叠部分图形的面积为S（S＞0），点D的运动时间为t秒.
(1)、线段AC的长为；(2)、当直线EF经过点D时，求t的值；(3)、求S与t的函数关系式，并直接写出t的取值范围.25. 在△ABC中，AB＝AC，点D平面内一点，M是BD中点，连接AM，作ME⊥AM.
(1)、如图1，若点E在CD的垂直平分线上，∠BAC＝m°，则求∠DEC的度数（用含m的式子表示）；(2)、如图2，当点D在CA延长线上，且DE⊥BC，若tan∠ABC＝k，则求 的值（用含k的式子表示）.26. 如图，在平面直角坐标系中，函数y＝ .
(1)、函数y的图象经过点（﹣1，0）.①求m值；
②当﹣2≤x≤0时，求函数值y的取值范围；
③当t﹣1≤x≤t+1时，函数y图象上的点到x轴的最大距离为2，求t的取值范围；
(2)、平面直角坐标系中有点A（﹣1，﹣2）、B（﹣1，4）、C（4，4）、D（4，﹣2）.若函数y的图象与四边形ABCD的边有两个交点时，直接写出m的取值范围.