辽宁省朝阳市朝阳县2021届九年级上学期数学期末考试试卷
试卷更新日期：2021-02-03 类型：期末考试
一、选择题（共10小题）.
-
1. 在下列汽车标志中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列方程中，是关于x的一元二次方程的是（ ）A、2x2﹣x﹣y2＝0 B、x（x﹣2）＝0 C、ax2+bx+c＝0 D、x﹣ ＝83. 方程x2﹣8x+2＝0，经过配方后，结果正确的是（ ）A、（x+4）2＝8 B、（x+4）2＝21 C、（x﹣4）2＝14 D、（x﹣4）2＝54. 某小组有若干人，新年大家互相发一条微信祝福，已知全组共发微信72条，则这个小组的人数为（ ）A、7人 B、8人 C、9人 D、10人5. 下列事件是随机事件的是（ ）A、菱形的对角线互相垂直 B、投一枚正方体骰子，朝上一面点数小于7 C、在只装了红球的不透明袋子里，摸出白球 D、射击运动员射击一次，命中靶心6. 如图，AB是⊙O的直径，点C，D在⊙O上， ＝ ，OD∥AC，下列结论错误的是（ ）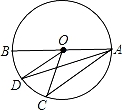
A、∠C＝∠D B、∠BOD＝∠COD C、∠BAD＝∠CAD D、∠BOD＝∠BAC7. 如图，△ABC绕点A按逆时针方向转动一个角度后成为△A′B′C′，在下列等式中：①BC＝B′C′；②∠BAB′＝∠CAC′；（3）∠ABC＝∠A′B′C′；④ .其中正确的个数是（ ）
A、3个 B、2个 C、1个 D、0个8. 如图，由六段相等的圆弧组成的三叶花，每段圆弧都是四分之一圆周，OA＝OB＝OC＝2，则这朵三叶花的面积为（ ）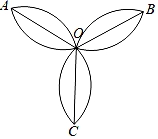
A、3π﹣3 B、3π﹣6 C、6π﹣3 D、6π﹣69. 如图，在平面直角坐标系中，过点A且与x轴平行的直线交抛物线y＝ （x+1）2于B，C两点，若线段BC的长为6，则点A的坐标为（ ）
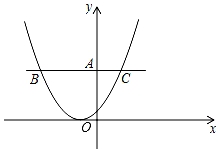A、（0，1） B、（0，4.5） C、（0，3） D、（0，6）10. 直线y＝bx+c与抛物线y＝ax2+bx+c（a＞0）在同一坐标系中大致图象可能是（ ）A、
B、
C、
D、
二、填空题：（每小题3分，共30分）
-
11. 已知关于 的一元二次方程 有实数根，则 的取值范围是 ．12. 关于x的方程x2+nx﹣6＝0有一个根为2，则方程的另一个根为.13. 如图，已知l1∥l2 ， 把一块含30°角的直角三角尺按如图所示的方式摆放，边BC在直线l2上，将△ABC绕点C顺时针旋转50°，则∠1的度数为.
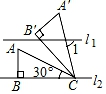14. 如图，⊙O的直径CD＝10，弦AB＝8，AB⊥CD，垂足为M，则CM的长为.
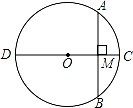15. 如图，一块矩形土地ABCD由篱笆围着，并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m（篱笆的厚度忽略不计），当AB＝m时，矩形土地ABCD的面积最大.
16. 已知A（0，y1），B（1，y2），C（4，y3）是抛物线y＝x2﹣3x上的三点，则y1 ， y2 ， y3的大小关系为.（用“＜”符号连接）17. 如图，小明从纸上剪下一个圆形和一个扇形纸片，用它们恰好能围成一个圆锥模型.若圆的半径为1，扇形的圆心角为120°，则此扇形的半径为.
18. 如图，点O为正方形的中心，点E、F分别在正方形的边上，且∠EOF＝90°，随机地往图中投一粒米，则米粒落在图中阴影部分的概率是 ．
19. 如图，长方形ABCD的两边BC，CD分别在x轴、y轴上，点C与原点重合，点A（﹣1，2），将长方形ABCD沿x轴无滑动向右翻滚，经过一次翻滚，点A对应点记为A1；经过第二次翻滚，点A对应点记为A2；…；依此类推，经过第2020次翻滚，点A对应点A2020坐标为.
20. 如图抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②a﹣b+c＜0；③b+2a＝0；④当y＜0时，x的取值范围是﹣1＜x＜3；⑤当x＜0时，y随x增大而增大；⑥方程ax2+bx+c＝2有两个不等的实数根，其中结论正确的结论的序号是.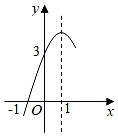
三、解答题（60分）
-
21. △ABC在平面直角坐标系xOy中的位置如图所示，点A（﹣2，3），点B（﹣4，0），点C（﹣1，1）为△ABC的顶点.
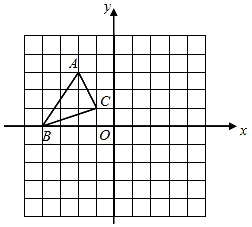
（1）作△ABC关于原点O成中心对称的△A1B1C1.
（2）将△A1B1C1向上平移5个单位，作出平移后的A2B2C2.
（3）在x轴上求作一点P，使PA+PA2的值最小，并求出点P的坐标.22. 如图，AB为⊙O的直径，C、D是⊙O上的点，P是⊙O外一点，AC⊥PD于点E，AD平分∠BAC.
(1)、求证：PD是⊙O的切线；(2)、若DE＝2，∠BAC＝60°，求⊙O的半径.23. 2020年疫情期间，某校为学生提供四种在线学习方式：在线阅读、在线听课、在线答疑、在线讨论，为了解学生的需求，对学生进行了“你最喜欢哪种在线学习方式的调查，调查结果制成两幅不完整统计图如图，根据图中信息回答问题：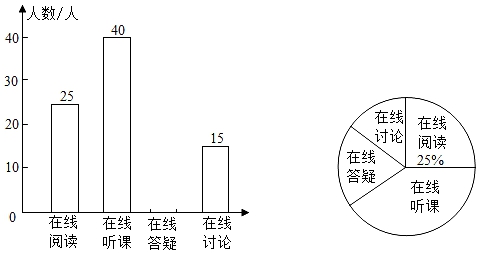
(1)、本次调查人数有人，在线答疑所在扇形的圆心角度数是；(2)、补全条形统计图；(3)、甲、乙两位同学都参加了在线学习，请用画树状图或列表的方法求出两名同学喜欢同一种在线学习方式的概率.24. 某工厂生产一批小家电，2018年的出厂价是144元，2019年，2020年连续两年改进技术，降低成本，2020年出厂价调整为100元．(1)、这两年出厂价下降的百分比相同，求平均下降率．(2)、某商场今年销售这批小家电的售价为140元时，平均每天可销售20台，为了减少库存，商场决定降价销售，经调查发现小家电单价每降低5元，每天可多售出10台，如果每天盈利1250元，单价应降低多少元？25. 如图，已知二次函数y＝﹣x2+bx+3的图象与x轴的两个交点为A（4，0）与点C，与y轴交于点B.
(1)、求此二次函数关系式和点C的坐标；(2)、请你直接写出△ABC的面积；(3)、在x轴上是否存在点P，使得△PAB是等腰三角形？若存在，请你直接写出点P的坐标；若不存在，请说明理由.