湖北省武汉市三校2021届九年级上学期数学期末联考试卷
试卷更新日期:2021-02-03 类型:期末考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 下列环保标志,既是轴对称图形,也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图所示,从上面看该几何体的形状图为( )
2. 如图所示,从上面看该几何体的形状图为( ) A、
A、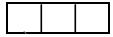 B、
B、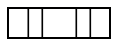 C、
C、 D、
D、 3. 有两把不同的钥匙和三把锁,其中两把钥匙分别能打开两把锁,且不能打开第三把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )A、 B、 C、 D、4. 若关于x的方程(k-1)x 2+4x+1=0有两不相等实数根,则k的取值范围是( )A、k≤5 B、k 5 C、k≤5且k≠1 D、k<5且k≠15. 如图,在⊙O中,弦AC∥半径OB,∠BOC=48°,则∠OAB的度数为( )
3. 有两把不同的钥匙和三把锁,其中两把钥匙分别能打开两把锁,且不能打开第三把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )A、 B、 C、 D、4. 若关于x的方程(k-1)x 2+4x+1=0有两不相等实数根,则k的取值范围是( )A、k≤5 B、k 5 C、k≤5且k≠1 D、k<5且k≠15. 如图,在⊙O中,弦AC∥半径OB,∠BOC=48°,则∠OAB的度数为( )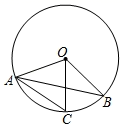 A、24° B、30° C、60° D、90°6. 竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ ,若小球经过 秒落地,则小球在上抛过程中,第( )秒离地面最高.A、 B、 C、 D、7. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( )
A、24° B、30° C、60° D、90°6. 竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ ,若小球经过 秒落地,则小球在上抛过程中,第( )秒离地面最高.A、 B、 C、 D、7. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中, 的顶点 的坐标分别为 、 , , ,函数 的图象经过点 ,则 的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中, 的顶点 的坐标分别为 、 , , ,函数 的图象经过点 ,则 的值为( )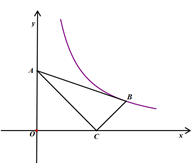 A、 B、 C、 D、259. 如图,在 中, ,点 为 的中点, , ,将 沿着 折叠后,点 落在点 处,则 的长为( )
A、 B、 C、 D、259. 如图,在 中, ,点 为 的中点, , ,将 沿着 折叠后,点 落在点 处,则 的长为( )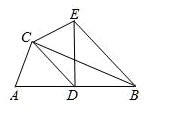 A、 B、4 C、7 D、10. 如图,抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;② ;③当 时,x的取值范围是 ;④当 时,y随x增大而增大;⑤若t为任意实数,则有 ,其中结论正确的个数是( )
A、 B、4 C、7 D、10. 如图,抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;② ;③当 时,x的取值范围是 ;④当 时,y随x增大而增大;⑤若t为任意实数,则有 ,其中结论正确的个数是( )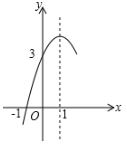 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(共6小题,每小题3分,共18分)
-
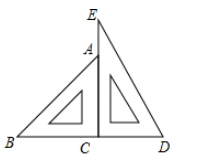
11. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺ABC绕着点C按逆时针方向旋转n°后(0<n<360 ),若ED⊥AB,则n的值是.
 12. 抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(x1 , 0),(x2 , 0),则x1+x2=.13. 在△ABC中,∠C=90°,∠A=30°,BC=4,D为边AB上的一点,若AD=2,则tan∠BDC的值为。14. 如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画 , 若 ,则阴影部分图形的周长为 结果保留 .
12. 抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(x1 , 0),(x2 , 0),则x1+x2=.13. 在△ABC中,∠C=90°,∠A=30°,BC=4,D为边AB上的一点,若AD=2,则tan∠BDC的值为。14. 如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画 , 若 ,则阴影部分图形的周长为 结果保留 .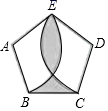 15. 如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y (k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为.
15. 如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y (k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为.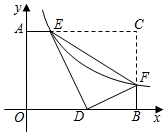 16. 如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值.
16. 如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值.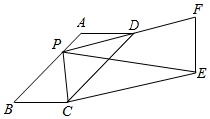
三、解答题(共8小题,共72分)
-
17. 小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪个人先下棋,规则如下:三人手中各持有一枚质地均匀的硬币,他们同时将手中硬币抛落到水平地面为一个回合,落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先下棋;若三枚硬币均为正面向上或反面向上,则不能确定其中两人先下棋.(1)、请你完成下面表示游戏一个回合所有可能出现的结果的树状图;(2)、求出一个回合能确定两人下棋的概率.18. 在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
 (1)、△ABC的中心对称图形,A点为对称中心;(2)、△ABC关于点P的位似△A′B′C′,且位似比为1:2;(3)、以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D .19. 已知关于x的一元二次方程x2-2 x+m=0有两个不相等的实数根.(1)、求实数m的最大整数值;(2)、在(1)的条件下,方程的实数根是 、 ,求代数式 的值.20. 如图,在圆O中,AB为直径,EF为弦,连接AF,BE交于点P,且EF2=PF•AF.
(1)、△ABC的中心对称图形,A点为对称中心;(2)、△ABC关于点P的位似△A′B′C′,且位似比为1:2;(3)、以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D .19. 已知关于x的一元二次方程x2-2 x+m=0有两个不相等的实数根.(1)、求实数m的最大整数值;(2)、在(1)的条件下,方程的实数根是 、 ,求代数式 的值.20. 如图,在圆O中,AB为直径,EF为弦,连接AF,BE交于点P,且EF2=PF•AF.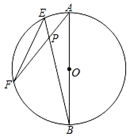 (1)、求证:F为弧BE的中点;(2)、若tan∠BEF= ,求cos∠ABE的值.21. 小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.(1)、求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;(2)、一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?(3)、为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.22. 如图,双曲线 与直线 相交于 ,点P是x轴上一动点.
(1)、求证:F为弧BE的中点;(2)、若tan∠BEF= ,求cos∠ABE的值.21. 小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.(1)、求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;(2)、一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?(3)、为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.22. 如图,双曲线 与直线 相交于 ,点P是x轴上一动点.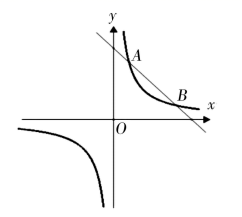 (1)、求双曲线 与直线 的解析式;(2)、当 时,直接写出x的取值范围;(3)、当 是等腰三角形时,求点P的坐标.23. 如图
(1)、求双曲线 与直线 的解析式;(2)、当 时,直接写出x的取值范围;(3)、当 是等腰三角形时,求点P的坐标.23. 如图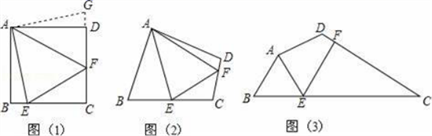 (1)、问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(1)、问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.(发现证明)小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(2)、(类比引申)如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.(3)、(探究应用)如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: =1.41, =1.73)24. 如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点C,抛物线 经过A,C两点,与x轴的另一交点为点B.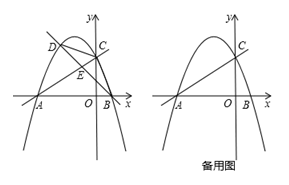 (1)、求抛物线的函数表达式;
(1)、求抛物线的函数表达式;
(2)、点D为直线AC上方抛物线上一动点;
①连接BC,CD,设直线BD交线段AC于点E, 的面积为S1 , 的面积为S2 , 求 的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得 中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.