河南省南阳市淅川县老城、大石桥、滔河三乡2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、选择题（共10小题）.

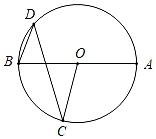
1. 已知2+ $\sqrt{3}$ 是关于x的一元二次方程x²﹣4x+m＝0的一个实数根，则实数m的值是（）

A、0 B、1 C、﹣3 D、﹣1

查看试题解析
2. 抛物线y＝2x²+c的顶点坐标为（0，1），则抛物线的解析式为（）

A、y＝2x²+1 B、y＝2x²﹣1 C、y＝2x²+2 D、y＝2x²﹣2

查看试题解析
3. 从数据﹣ $\frac{1}{2}$ ，﹣6，1.2，π，﹣ $\sqrt{2}$ ，0.010010001…中任取一个数，则该数为无理数的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 下列图形中，任意两个图形一定是相似图形的是（）

A、三角形 B、平行四边形 C、抛物线 D、圆

查看试题解析
5. 如图，AB是⊙O的直径，点D在⊙O上，若∠AOC＝120°，则∠D的度数是（）

A、20° B、30° C、40° D、45°

查看试题解析
6. 如图，在Rt△ABC中，∠ACB＝90°，如果AC＝4，cosB＝ $\frac{3}{5}$ ，那么BC等于（）

A、3 B、4 C、5 D、6

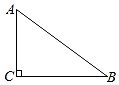查看试题解析
7. 若二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是（）

A、x＜3 B、x≠3 C、x≤3 D、x≥3

查看试题解析
8. 下列四组线段中，不构成比例线段的一组是 ( )

A、 $1 c m ， 2 c m ， 3 c m ， 6 c m$ B、 $2 c m ， 3 c m ， 4 c m ， 6 c m$ C、 $1 c m ， \sqrt{2} c m ， \sqrt{3} c m ， \sqrt{6} c m$ D、 $1 c m ， 2 c m ， 3 c m ， 4 c m$

查看试题解析
9. 正方形外接圆的半径为4，则其内切圆的半径为（）

A、2 $\sqrt{2}$ B、 $\sqrt{2}$ C、1 D、 $\frac{\sqrt{2}}{2}$

查看试题解析
10. 抛物线y＝ax²+bx+c（a＞0）过点（1，0）和点（0，﹣3），且顶点在第三象限，设m＝a﹣b+c，则m的取值范围是（）

A、﹣6＜m＜0 B、﹣6＜m＜﹣3 C、﹣3＜m＜0 D、﹣3＜m＜﹣1

查看试题解析

二、填空题（共5小题）.

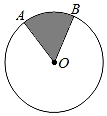
11. 如图，在半径为6的⊙O中，随意向圆内投掷一个小球，经过大量重复投掷后发现，小球落在阴影部分的概率稳定在 $\frac{1}{6}$ ，则 $\overset{⌢}{A B}$ 的长约为.（结果保留π）

查看试题解析
12. 圆锥的侧面展开图的圆心角是120°，其底面圆的半径为3cm，则其侧面积为.

查看试题解析
13. 若x₁ ， x₂方程x²﹣4x﹣2021＝0的两个实数根，则代数式x₁²﹣2x₁+2x₂的值等于.

查看试题解析
14. 如图，点A，B，C为正方形网格中的3个格点，则tan∠ACB＝.

查看试题解析
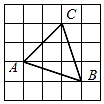15. 如图，点C为半圆的中点，AB是直径，点D是半圆上一点，AC，BD交于点E，若AD＝1，BD＝7，则CE的长为.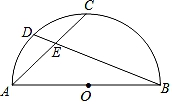

查看试题解析

三、解答题（本大题共8个小题，满分75分）

16. 在一个不透明的口袋中有标号为1，2，3，4的四个小球，除数字不同外，小球没有任何区别，摸球前先搅拌均匀，每次摸一个球.

(1)、摸出一个球，摸到标号为奇数的概率为.

(2)、从袋中不放回地摸两次，用列表或树状图求出两球标号数字为偶数的概率.

查看试题解析
17.

(1)、计算3tan30°﹣tan45°+2cos30°+4sin60°；

(2)、计算： $\sqrt{12}$ +（π﹣2019）⁰﹣（ $\sqrt{3}$ +1）²；

(3)、解方程： $\frac{x - 1}{2}$ ＝ $\frac{2 x + 3}{3}$ .

查看试题解析
18. 如图，在△ABC中，CD是边AB上的高，且 $\frac{A D}{C D}$ ＝ $\frac{C D}{B D}$ ，

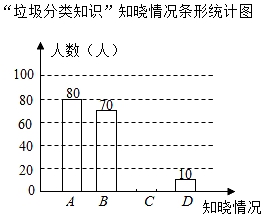
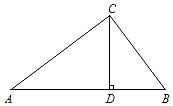(1)、求∠ACB的大小；

(2)、求证BC²＝BD•AB.

查看试题解析

19. 某学校为了解同学们对“垃圾分类知识”的知晓情况，某班数学兴趣小组随机调查了学校的部分同学，根据调查情况制作的统计图表的一部分如图所示：

“垃圾分类知识”知晓情况统计表

知晓情况	频数	频率
A.非常了解	80	n
B.比较了解	70	0.35
C.基本了解	m	0.20
D.不太了解	10	0.05

(1)、本次调查取样的样本容量是，表中n的值是.

(2)、根据以上信息补全条形统计图.

(3)、若基本了解和不太了解都属于“不达标”等级，根据调查结果，请估计该校1800名同学中“不达标”的学生有多少人？

查看试题解析

20. 如图，从A城市到B城市要翻过一座大山，现需要打通隧道，修建高铁方便两地出行，已知在A城市的北偏东30°方向和B城市的北偏西67°方向有一C地，A ， C相距230km ，求A ， B两个城市之间的距离．（参考数据：sin67°≈ $\frac{12}{13}$ ，cos67°≈ $\frac{5}{13}$ ，tan67°≈ $\frac{12}{5}$ ， $\sqrt{3}$ ≈1.7，结果精确到1km）

查看试题解析
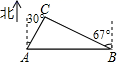21. 某果农在其承包的果园中种植了60棵桔子树，每棵桔子树的产量是100kg，果农想增加桔子树的棵数来增产，但增加果树会导致每棵树的光照减少，使得单棵果树产量减少，试验发现每增加1棵桔子树，单棵桔子树的产量减少0.5kg．

(1)、在投入成本最低的情况下，增加多少棵桔子树时，可以使果园总产量达到6650kg？

(2)、设增加x棵桔子树，考虑实际增加桔子树的情况，10≤x≤40，请你计算一下，果园总产量最多为多少kg，最少为多少kg？

查看试题解析
22. 如图，四边形ABCD内接于⊙O，AC为⊙O的直径，D为弧AC的中点，过点D作DE∥AC，交BC的延长线于点E.

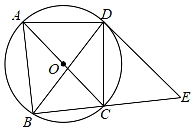(1)、判断DE与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径为7，AB＝10，求CE的长.

查看试题解析
23. 抛物线y＝ax²+bx﹣6a与x轴交于A，B两点，且A（﹣2，0），抛物线的顶点为P.

(1)、求点P的坐标；（用只含a的代数式表示）

(2)、若﹣8≤a≤﹣5，求△ABP面积的最大值；

(3)、当a＝1时，把抛物线y＝ax²+bx﹣6a位于x轴下方的部分沿x轴向上翻折，其余部分保持不动，得到新的函数图象.若直线y＝﹣x+t与新的函数图象至少有3个不同的交点，求t的取值范围.

查看试题解析