浙江省温州市鹿城区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、单选题

1. sin60°的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析
2. 抛物线 $y = - {(x + 2)}^{2} + 1$ 的顶点坐标为（）

A、 $(2, 1)$ B、 $(2, - 1)$ C、 $(- 2, - 1)$ D、 $(- 2, 1)$

查看试题解析
3. 某同学连续抛掷硬币2次，都是正面朝上，则抛掷第3次出现正面朝上的概率为（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{8}$ D、 $\frac{1}{6}$

查看试题解析
4. 如图，在2×3的方格中，画有格点△ABC，下列选项的方格中所画格点三角形（阴影部分）与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
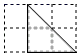5. 如图，直线l₁、l₂、l₃分别交直线l₄于点A、B、C，交直线l₅于点D、E、F，且 $l_{1} // l_{2} // l_{3}$ ，已知DE：DF=3：7，BC=14，则AB的长为（）

A、10.5 B、6 C、7 D、8

查看试题解析
6. 如图，在⊙O中，点B是弧AC上的一点，∠AOC=140°，则∠ABC的度数为（）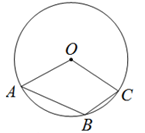

A、70° B、110° C、120° D、140°

查看试题解析
7. 点 $A (- 1, y_{1})$ ， $B (1, y_{2})$ ， $C (2, y_{3})$ 是二次函数 $y = a x^{2} - 2 a x + 3$ $(a > 0)$ 图象上的三点，则y₁ ， y₂ ， y₃的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
8. 在正方形网格中，∠AOB如图所示放置，则sin∠AOB的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{85}}{10}$

查看试题解析
9. 如图，一把直角三角板的顶点A、B在⊙O上，边BC、AC与⊙O交于点D、E，已知∠C=30°，则∠AED的大小为（）

A、90° B、100° C、110° D、120°

查看试题解析
10. 已知抛物线 $y = - 2 x^{2} + b x + c$ 与x轴交于点A，B两点（A在原点O左侧，B在原点O右侧），与y轴交于点C，若OC=OB，则点A的横坐标为（）

A、 $\frac{b}{2}$ B、 $- \frac{1}{2}$ C、 $- \frac{2}{c}$ D、-2

查看试题解析

二、填空题

11. 已知 $\frac{x}{y} = \frac{2}{3}$ ，则 $\frac{x + 2 y}{y}$ =.

查看试题解析
12. 已知一个扇形的半径长是4cm，圆心角为45°，则这个扇形的面积是cm².

查看试题解析
13. 若某斜面的坡度为 $1 : \sqrt{3}$ ，则该坡面的坡角为.

查看试题解析
14. 已知二次函数 $y = a x^{2} + b x + c$ ，观察下表：

x的值

0

4

6

ax²+bx+c的值

3

3

5

则当x=-2时，y= .

查看试题解析
15. 如图，在△ABC中，∠ABC＝90°，AB＝6，BC＝4，P是△ABC的重心，连结BP，CP，则△BPC的面积为.

查看试题解析
16. △ABC内接于⊙O，且满足AB＞AC，连结AO，D，E分别是BC，AO的中点，且OD=OE，若∠ODE等于10°，则∠B等于.

查看试题解析

三、解答题

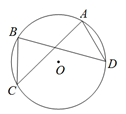
17. 如图，A、B、C在⊙O上，若 $B C = A D$ ，求证： $A C = B D$ .

查看试题解析
18. 一个不透明的袋子中装有汉子“清”“华”“大”“学”的4个小球，除汉字不同之外，小球材质、大小、形状完全相同，每次摸球前先搅均匀再摸球.

(1)、求从袋中摸出一个球，则球上的汉字刚好是“大”的概率是；

(2)、从袋中任取一球，不放回，再从袋中任取一球，请用树状图或列表法，求取出的两个球上的汉字能组成“清华”的概率.

查看试题解析
19. 如图， $Δ A B C$ 是9×9的正方形网格中的格点三角形（顶点在格点上），请在正方形的网格上按下列要求画一个与 $Δ A B C$ 相似的格点三角形.

(1)、在图1中画 $Δ A_{1} B_{1} C_{1}$ 使 $Δ A_{1} B_{1} C_{1}$ 的周长是 $Δ A B C$ 的周长的2倍；

(2)、在图1中画 $Δ A_{2} B_{2} C_{2}$ 使得 $Δ A_{2} B_{2} C_{2}$ 的面积是 $Δ A B C$ 的面积的5倍.

查看试题解析
20. 如图，广场上空有一个气球A，地面上B，C，D在同一条直线上，BC=20米，在点B，C分别测得气球A的仰角∠ABD为45°，∠ACD为56°，求气球A离地面的高度AD（精确到0.1m）.(参考数据sin56°≈0.829；cos56°≈0.559；tan56°≈1.482)

查看试题解析
21. 如图，在矩形ABCD中，F为CD上的点，AF⊥BD且AF，BD相交于点E，

(1)、求证： $△$ ABD∽ $△$ DAF；

(2)、若AB＝8，BG＝3AD，求AG的长.

查看试题解析
22. 已知二次函数 $y = x^{2} + b x + c$ 的对称轴是直线 $x = 2$ ，且经过点 $A (- 1, 0)$ .

(1)、求二次函数的解析式；

(2)、若点P（m，n）在该二次函数图象上，且点P到y轴的距离小于3，求n的取值范围.

查看试题解析
23. 某公司有一块如图所示的平行四边形ABCD的绿化地，中间四边形EFGH是正方形，种上甲类花； $△$ AGD和 $△$ BEC是全等的等腰直角三角形，种上乙类花； $△$ ABH和 $△$ CDF是全等的直角三角形，种上丙类花；三类花的价格如下表：

花的种类

甲

乙

丙

价格（元/米²）

200

100

150

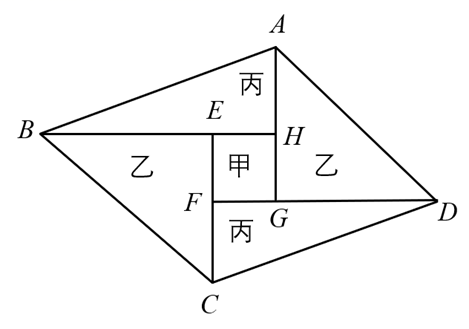
已知AH＝3米，设BE的长为x米，绿化的总费用为y元.

(1)、用含有x的代数式表示：EF＝，FD＝；

(2)、求y关于x的函数解析式及x的取值范围；

(3)、如果FD的长比CF至少多4米，求总费用y的最小值.

查看试题解析
24. 如图，在等腰直角三角形△ABC，∠ABC=90°，AB=6，P是射线AB上一个动点，连接CP，以CP为斜边构造等腰直角△CDP（C、D、P按逆时针方向），M为CP的中点，连接AD，MB.

(1)、当点P在线段AB上运动时，求证：△CDA∽△CMB；

(2)、设 $A P = x$ ，△ADP的面积为y.
①当 $0 < x < 12$ 时，求y关于x的函数表达式；

②记D关于直线AC的对称点为 $D^{'}$ ，若 $D^{'}$ 在△APC的内部，求y的取值范围.

查看试题解析

x的值	0	4	6
ax²+bx+c的值	3	3	5

花的种类	甲	乙	丙
价格（元/米²）	200	100	150