辽宁省沈阳市皇姑区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、单选题
-
1. 的值等于( )A、 B、 C、 D、12. 如图所示几何体的左视图是( )
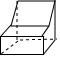 A、
A、 B、
B、 C、
C、 D、
D、 3. 方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. a,b,c,d是成比例线段,其中 , , ,则线段d为( )A、1cm B、2cm C、4cm D、9cm5. 已知函数 ,则( )A、当 时,y随x的增大而增大 B、当 时,y随x的增大而减小 C、当 时,y随x的增大而增大 D、当 时,y随x的增大而减小6. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
3. 方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. a,b,c,d是成比例线段,其中 , , ,则线段d为( )A、1cm B、2cm C、4cm D、9cm5. 已知函数 ,则( )A、当 时,y随x的增大而增大 B、当 时,y随x的增大而减小 C、当 时,y随x的增大而增大 D、当 时,y随x的增大而减小6. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )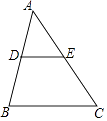 A、6 B、12 C、18 D、247. 如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A、6 B、12 C、18 D、247. 如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )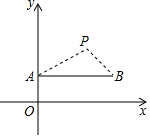 A、3 B、5 C、6 D、78. 在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球为白球的概率是 , 则黄球的个数为()A、16 B、12 C、8 D、49. 如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A、3 B、5 C、6 D、78. 在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球为白球的概率是 , 则黄球的个数为()A、16 B、12 C、8 D、49. 如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )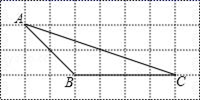 A、 B、 C、 D、10. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、
A、 B、 C、 D、10. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、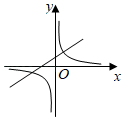 B、
B、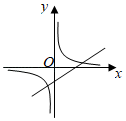 C、
C、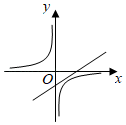 D、
D、
二、填空题
-
11. 已知 ,则 .12. 若 ,且 与 的面积之比为 ,则 与 的相似比为.13. 已知:如图, , ,以原点O为位似中心,相似比 ,把 在点O另一侧缩小,则点E的对应点 的坐标为 .
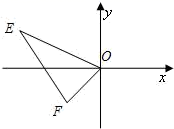 14. 如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长.
14. 如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长.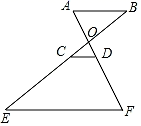 15. 由于新能源汽车越来越多,为了解决充电难的问题,现对一面积为 的矩形停车场进行改造.将该矩形停车场的长减少20m,减少的这部分区域用于修建电动汽车充电桩,原停车场的剩余部分就变成了正方形,则原停车场的长是.16. 等腰 中, , ,以AC为边作等边 ,则点B到CD的距离为.
15. 由于新能源汽车越来越多,为了解决充电难的问题,现对一面积为 的矩形停车场进行改造.将该矩形停车场的长减少20m,减少的这部分区域用于修建电动汽车充电桩,原停车场的剩余部分就变成了正方形,则原停车场的长是.16. 等腰 中, , ,以AC为边作等边 ,则点B到CD的距离为.三、解答题
-
17. 计算: .18. 解方程: .19. 有四张正面分别写有数字:20,15,10,5的卡片,背面完全相同,将卡片洗匀后背面朝上.放在桌面上小明先随机抽取一张,记下牌面上的数字(不放回),再从剩下的卡片中随机抽取一张,记下牌面上的数字.如果卡片上的数字分别对应价值为20元,15元,10元,5元的四件奖品,请用列表或画树状图法求小明两次所获奖品总值不低于30元的概率?20. 如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
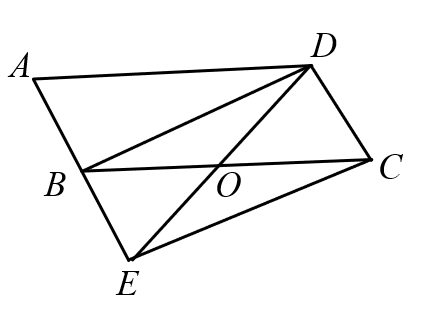 (1)、求证:四边形BECD是平行四边形;(2)、若 ,则当 °时,四边形BECD是菱形.21. 如图武汉绿地中心,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高636m,是目前湖北省第二高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα= ,在顶端E点测得A的仰角为45°,AE=140 m.
(1)、求证:四边形BECD是平行四边形;(2)、若 ,则当 °时,四边形BECD是菱形.21. 如图武汉绿地中心,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高636m,是目前湖北省第二高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα= ,在顶端E点测得A的仰角为45°,AE=140 m.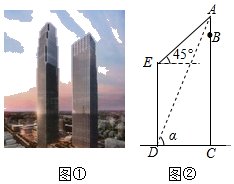 (1)、求两楼之间的距离CD;(2)、求发射塔AB的高度.22. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A,B,C的坐标分别为 , , .反比例函数 的函数图象经过点D,点P是反比例函数上一动点,直线PC的解折式为: .
(1)、求两楼之间的距离CD;(2)、求发射塔AB的高度.22. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A,B,C的坐标分别为 , , .反比例函数 的函数图象经过点D,点P是反比例函数上一动点,直线PC的解折式为: .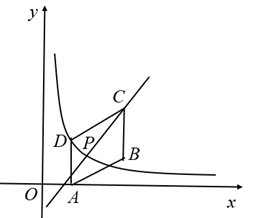 (1)、求反比例函数的解析式;(2)、对于一次函数 ,当y随x的增大而增大时,直接写出点P的横坐标x的取值范围.23. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位及养老建筑不断增加。(1)、该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个,求该市这两年(从2017年底到2019年底)拥有的养老床位数的平均年增长率;(2)、该市某社区今年准备新建一养老中心,如果计划赡养200名老人,建筑投入平均5万元/人,且计划赡养的老人每增加5人,建筑投入平均减少1000元/人,那么新建该养老中心需申报的最高建筑投入是多少?24. 在矩形ABCD中,点E在边BC上,连接AE.
(1)、求反比例函数的解析式;(2)、对于一次函数 ,当y随x的增大而增大时,直接写出点P的横坐标x的取值范围.23. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位及养老建筑不断增加。(1)、该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个,求该市这两年(从2017年底到2019年底)拥有的养老床位数的平均年增长率;(2)、该市某社区今年准备新建一养老中心,如果计划赡养200名老人,建筑投入平均5万元/人,且计划赡养的老人每增加5人,建筑投入平均减少1000元/人,那么新建该养老中心需申报的最高建筑投入是多少?24. 在矩形ABCD中,点E在边BC上,连接AE.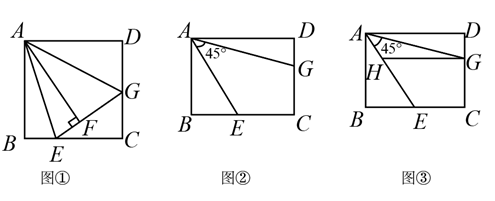 (1)、如图①,当矩形ABCD为正方形时,将 沿AE翻折得到 ,连接EF并延长交边CD于点G,连接AG.求证: ;(2)、如图②,在矩形ABCD的边CD上取一点G,连接AG,使 .
(1)、如图①,当矩形ABCD为正方形时,将 沿AE翻折得到 ,连接EF并延长交边CD于点G,连接AG.求证: ;(2)、如图②,在矩形ABCD的边CD上取一点G,连接AG,使 .①若 , , ,则 (直接填空);
②过点G作 ,交AE于点H,如图③,若 ,请直接写出线段GH、BE、DG之间的数量关系.
25. 如图①,在平面直角坐标系中,矩形ABCO的顶点O为坐标原点,点A在x轴上,点C在y轴上,点B的坐标为 ,点C的坐标为 .抛物线 经过点B和点C,连接AC,点M是线段AC上一动点,连接OM,点N在线段AM上(不与点M重合),连接ON并延长交边AB于点E,连接ME.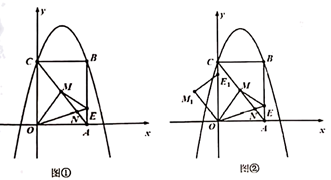 (1)、求抛物线的表达式;(2)、当 时,求线段CN的长;(3)、在(2)的条件下,将 绕点O逆时针旋转得到 ,使 落在线段OC上,如图②当 时,过点C作 交抛物线于点P(点C除外),请直接写出点P的横坐标.
(1)、求抛物线的表达式;(2)、当 时,求线段CN的长;(3)、在(2)的条件下,将 绕点O逆时针旋转得到 ,使 落在线段OC上,如图②当 时,过点C作 交抛物线于点P(点C除外),请直接写出点P的横坐标.