辽宁省沈阳市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、选择题(本大题共10小题,共20.0分)
-
1. 2cos60°的值是( )A、 B、 C、 D、12. 如图,图中的几何体中,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各组中的四条线段是成比例线段的是( )A、4cm、1cm、2cm、1cm B、1cm、2cm、3cm、4cm C、25cm、35cm、45cm、55cm D、1cm、2cm、20cm、40cm4. 一元二次方程 的根的情况是( )A、有两个相等的实根 B、没有实数根 C、有两个不相等的实根 D、无法确定5. 对于二次函数 ,下列说法正确的是( )A、图象开口向下 B、图象和y轴交点的纵坐标为-3 C、 时,y随x的增大而减小 D、图象的对称轴是直线6. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、7. 如图,在 中, , , ,点D、E分别是BC、CA的中点,则 的周长为( )
3. 下列各组中的四条线段是成比例线段的是( )A、4cm、1cm、2cm、1cm B、1cm、2cm、3cm、4cm C、25cm、35cm、45cm、55cm D、1cm、2cm、20cm、40cm4. 一元二次方程 的根的情况是( )A、有两个相等的实根 B、没有实数根 C、有两个不相等的实根 D、无法确定5. 对于二次函数 ,下列说法正确的是( )A、图象开口向下 B、图象和y轴交点的纵坐标为-3 C、 时,y随x的增大而减小 D、图象的对称轴是直线6. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、7. 如图,在 中, , , ,点D、E分别是BC、CA的中点,则 的周长为( ) A、15 B、18 C、20 D、228. 在一个不透明的盒子中装有m个除颜色外完全相同的球,这m个球中只有3个红球,从中随机摸出一个小球,恰好是红球的概率为 ,那么m的值是( )A、12 B、15 C、18 D、219. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A、15 B、18 C、20 D、228. 在一个不透明的盒子中装有m个除颜色外完全相同的球,这m个球中只有3个红球,从中随机摸出一个小球,恰好是红球的概率为 ,那么m的值是( )A、12 B、15 C、18 D、219. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )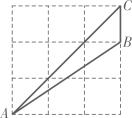 A、 B、 C、 D、10. 一次函数 和反比例函数 在同一直角坐标系中的图象可能是A、
A、 B、 C、 D、10. 一次函数 和反比例函数 在同一直角坐标系中的图象可能是A、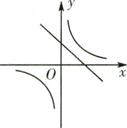 B、
B、 C、
C、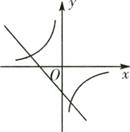 D、
D、
二、填空题(本大题共6小题,共18.0分)
-
11. 如果 ≠0,那么 = .12. 已知 ∽ ,相似比为3:1,若 的面积为5,则 的面积为 .13. 已知在平面直角坐标系中,点 、 、 ,以原点为位似中心将 缩小,位似比为1:2,则点B的对应点的坐标为 .14. 如图,已知AD、BC相交于点O, ,如果 , , ,那么 .
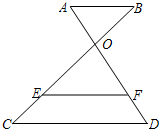 15. 如图,矩形ABCD是由三个矩形拼接成的,如果 ,阴影部分的面积是 ,另外两个小矩形全等,那么小矩形的长为cm.
15. 如图,矩形ABCD是由三个矩形拼接成的,如果 ,阴影部分的面积是 ,另外两个小矩形全等,那么小矩形的长为cm. 16. 如图,已知等边 的边长是6,点D在AC上,且 延长BC到E,使 ,连接 点F,G分别是AB,DE的中点,连接FG,则FG的长为.
16. 如图,已知等边 的边长是6,点D在AC上,且 延长BC到E,使 ,连接 点F,G分别是AB,DE的中点,连接FG,则FG的长为.
三、解答题(本大题共9小题,共82.0分)
-
17. 计算: .18. 解方程(1)、 ;(2)、 .19. 如图是一副扑克牌中的三张牌,将它们正面向下洗匀,甲同学从中随机抽取一张牌后放回,洗匀,乙同学再从中随机抽取一张牌,用画树状图或列表的方法,求抽出的两张牌中牌面上的数字都是偶数的概率.
 20. 如图,在平行四边形ABCD中, , , ,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
20. 如图,在平行四边形ABCD中, , , ,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.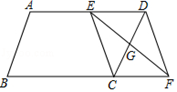 (1)、求证:四边形CEDF是平行四边形;(2)、① cm时,四边形CEDF是矩形.
(1)、求证:四边形CEDF是平行四边形;(2)、① cm时,四边形CEDF是矩形.② cm时,四边形CEDF是菱形.
21. 如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为 ,点C的仰角为 ,点P到建筑物的距离为 米,求点B与点C之间的距离.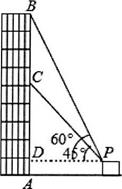 22. 已知反比例函数 为常数 的图象在第一、三象限.
22. 已知反比例函数 为常数 的图象在第一、三象限. (1)、求m的取值范围;(2)、如图,若该反比例函数的图象经过平行四边形ABOD的顶点D,点A、B的坐标分别为 , 求出函数解析式.23. 某商店准备进一批季节性小家电,经调查一种进价每个为2元的小家电的销售情况,若每个小家电售价为5元,每天能卖出500个,而且这种小家电的售价每上涨 元,其销售量减少10个.(1)、如果每天要实现1575元的销售利润,那该如何定价?(2)、如果每天要实现销售利润最大,那该如何定价?24. 已知正方形ABCD,点M边AB的中点.
(1)、求m的取值范围;(2)、如图,若该反比例函数的图象经过平行四边形ABOD的顶点D,点A、B的坐标分别为 , 求出函数解析式.23. 某商店准备进一批季节性小家电,经调查一种进价每个为2元的小家电的销售情况,若每个小家电售价为5元,每天能卖出500个,而且这种小家电的售价每上涨 元,其销售量减少10个.(1)、如果每天要实现1575元的销售利润,那该如何定价?(2)、如果每天要实现销售利润最大,那该如何定价?24. 已知正方形ABCD,点M边AB的中点.
 (1)、如图1,点G为线段CM上的一点,且 ,延长AG,BG分别与边BC,CD交于点E,F.
(1)、如图1,点G为线段CM上的一点,且 ,延长AG,BG分别与边BC,CD交于点E,F.求证: ;
直接写出 的值.
(2)、如图2,在边BC上取一点E,满足 ,连接AE交CM于点G,连接BG并延长交CD于点F,求 的值.25. 如图,抛物线 与x轴交于点 和 ,与y轴交于点C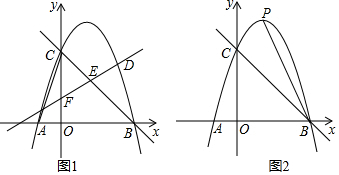 (1)、求抛物线的表达式;(2)、如图1,若点F在线段OC上,且 ,经入过点F的直线在第一象限内与抛物线交于点D,与线段BC交于点E,求 的最大值;(3)、如图2,若P为抛物线的顶点,动点Q在抛物线上,当 时,请直接写出点Q的坐标.
(1)、求抛物线的表达式;(2)、如图1,若点F在线段OC上,且 ,经入过点F的直线在第一象限内与抛物线交于点D,与线段BC交于点E,求 的最大值;(3)、如图2,若P为抛物线的顶点,动点Q在抛物线上,当 时,请直接写出点Q的坐标.