河南省驻马店市上蔡县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-02-03 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分）

1. 下列式子正确的是（）

A、 $\sqrt{3^{2}} = \pm 3$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $3 \sqrt{3} - \sqrt{3} = 3$ D、 ${(- \sqrt{3})}^{2} = 3$

查看试题解析
2. 已知一元二次方程 $x^{2} + k x - 3 = 0$ 有一个根为1，则 $k$ 的值为（）

A、-2 B、2 C、-4 D、4

查看试题解析
3. 如图，已知 $△ A C D$ ∽ $△ B C A$ ，若 $C D = 4$ ， $D B = 5$ ，则AC等于（）

A、3 B、4 C、5 D、6

查看试题解析
4. 如图是一个3×2的长方形网格，组成网格的小长方形长为宽的2倍，△ABC的顶点都是网格中的格点，则sin∠BAC的值（）

A、 $\frac{6 \sqrt{13}}{65}$ B、 $\frac{5 \sqrt{13}}{78}$ C、 $\frac{\sqrt{13}}{13}$ D、 $\frac{5 \sqrt{13}}{26}$

查看试题解析
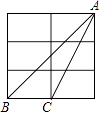5. 如果点 $M (- 2, y_{1})$ ， $N (- 1, y_{2})$ 在抛物线 $y = - x^{2} + 2 x$ 上，那么下列结论正确的是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} \leq y_{2}$ D、 $y_{1} \geq y_{2}$

查看试题解析
6. 二次函数 $y = {(x - 2)}^{2} + 1$ 的图象上的顶点坐标是（）

A、 $(- 2, - 1)$ B、 $(2, 1)$ C、 $(1, 2)$ D、 $(- 1, - 2)$

查看试题解析
7. 在一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4．若随机摸出一个小球后不放回，再随机摸出一个小球，则两次取出小球标号的和等于5的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{3}{16}$

查看试题解析
8. 如图， $⊙ O$ 中， $\overset{⌢}{A B} = \overset{⌢}{A C}$ ， $∠ A B C = 70 °$ ．则 $∠ B O C$ 的度数为（）

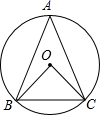A、100° B、90° C、80° D、70°

查看试题解析
9. 如图，AB是半圆O的直径，C、D是半圆O上的两点， $O D / / B C$ ，OD与AC交于点 $E .$ 下列结论不一定成立的是（）

A、 $△ A O D$ 是等边三角形 B、 $\overset{⌢}{A D} = \overset{⌢}{C D}$ C、 $∠ A C B = 90 °$ D、 $O E = \frac{1}{2} B C$

查看试题解析
10. 如图，菱形ABCD中， $A B = 2$ ， $∠ B = 60 °$ ，M为AB的中点.动点P在菱形的边上从点B出发，沿 $B \to C \to D$ 的方向运动，到达点D时停止.连接MP，设点P运动的路程为x， $M P^{2} = y$ ，则表示y与x的函数关系的图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共5小题，共15.0分）

11. 计算： $\sin 45^{°} =$ ．

查看试题解析
12. 已知 $x = 4$ 是一元二次方程 $x^{2} - 3 x + c = 0$ 的一个根，则另一个根为.

查看试题解析
13. 如图，在平行四边形ABCD中，E为边BC上一点，AC与DE相交于点F，若 $C E = 2 E B$ ， $S_{△ A F D} = 27$ ，则 $S_{△ E F C}$ 等于.

查看试题解析
14. 如图，在直角坐标系中，点 $E (- 4 ， 2)$ ， $F (- 2 ， - 2)$ ，以O为位似中心，按2：1的相似比把 $△ E F O$ 缩小为 $△ E' F' O$ ，则点E的对应点 $E'$ 的坐标为 .

查看试题解析
15. 如图，在平面直角坐标系中，抛物线 $y = x^{2} - 2 x + 2$ 交y轴于点A，直线AB交x轴正半轴于点B，交抛物线的对称轴于点C，若 $O B = 2 O A$ ，则点C的坐标为 .

查看试题解析

三、解答题（本大题共8小题，共75.0分）

16. 先化简，再求值： $(2 - \frac{x - 1}{x + 1}) \div \frac{x^{2} + 6 x + 9}{x^{2} - 1}$ ，其中 $x = 3 \tan 30 ° - 3$ ．

查看试题解析
17. 有4张看上去无差别的卡片，上面分别写有数 $- 1$ ，2，5，8.

(1)、随机抽取一张卡片，则抽取到的数是偶数的概率为；

(2)、随机抽取一张卡片后，放回并混在一起，再随机抽取一张，请用画树状图或列表法，求抽取出的两数之差的绝对值大于3的概率.

查看试题解析
18. 如图，在⊙O中，AC与BD是圆的直径，BE⊥AC，CF⊥BD，垂足分别为E、F

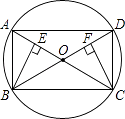(1)、四边形ABCD是什么特殊的四边形？请判断并说明理由；

(2)、求证：BE=CF．

查看试题解析
19. 已知关于x的方程 $m x^{2} + 2 (m + 1) x + m = 0$ 有两个实数根.

(1)、求m的取值范围；

(2)、若方程的两个实数根的平方和为6，求m的值.

查看试题解析
20. 在B港有甲、乙两艘渔船，若甲船沿北偏东 $60 °$ 方向以每小时8海里的速度前进，乙船沿南偏东 $30 °$ 方向以每小时15海里的速度前进，2小时后，甲船到M岛，乙船到P岛，求两岛之间的距离.

查看试题解析
21. 某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且利润率不得高于 $50 % .$ 经市场调查，每天的销售量 $y ($ 千克 $)$ 与每千克售价 $x ($ 元 $)$ 满足一次函数关系，部分数据如下表：

售价x $($ 元 $/$ 千克 $)$

45

50

55

销售量y $($ 千克 $)$

110

100

90

(1)、求y与x之间的函数表达式，并写出自变量的范围；

(2)、设每天销售该商品的总利润为 $W ($ 元 $)$ ，求W与x之间的函数表达式 $($ 利润 $=$ 收入 $-$ 成本 $)$ ，并求出售价为多少元时每天销售该商品所获得最大利润，最大利润是多少？

查看试题解析
22. 如图，四边形ABCD是正方形，G是BC的延长线上一点，连接AG交CD于点H， $B E ⊥ A G$ 于点E， $D F ⊥ A G$ 于点F.

(1)、证明： $△ A B E$ ≌ $△ D A F$ ；

(2)、若 $∠ A G B = 30 °$ ， $B G = 4 \sqrt{3}$ ，求EF的长；

(3)、若H为CD的中点，请直接写出线段EH与HG的数量关系.

查看试题解析
23. 抛物线 $y = a x^{2} - 2 a x - 3 a$ 与x轴交于A、B两点 $($ 其中A在左侧，B在右侧，且经过点 $C (2 ， 3)$ .

(1)、求抛物线解析式；

(2)、点D为线段AC上一动点 $($ 与A、C不重合 $)$ ，过D作直线 $E F / / y$ 轴交抛物线于 $E .$ 交x轴于F，请求出当DE最大时的E点坐标和DF长；

(3)、是否存在点E，使 $△ D C E$ 为等腰直角三角形？若存在，请求出点D的坐标；若不存在，请说明理由.

查看试题解析

售价x $($ 元 $/$ 千克 $)$	45	50	55
销售量y $($ 千克 $)$	110	100	90