河南省信阳市商城县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-02-03 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 小强同学从-1,0,1,2,3,4这六个数中任选一个数,满足不等式 的概率是()A、 B、 C、 D、3. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、4. 在同一坐标系中,一次函数 与二次函数 的图象可能是( ).A、
2. 小强同学从-1,0,1,2,3,4这六个数中任选一个数,满足不等式 的概率是()A、 B、 C、 D、3. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、4. 在同一坐标系中,一次函数 与二次函数 的图象可能是( ).A、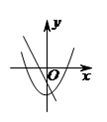 B、
B、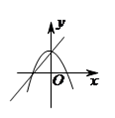 C、
C、 D、
D、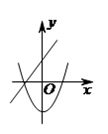 5. 一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是( )A、48π B、45π C、36π D、32π6. 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ).A、20% B、40% C、18% D、36%7. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
5. 一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是( )A、48π B、45π C、36π D、32π6. 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ).A、20% B、40% C、18% D、36%7. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )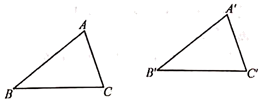 A、①④ B、②③ C、②④ D、③④8. 如图,四边形 内接于⊙ , 交 的延长线于点 ,若 平分 , ,则 ( )
A、①④ B、②③ C、②④ D、③④8. 如图,四边形 内接于⊙ , 交 的延长线于点 ,若 平分 , ,则 ( ) A、 B、 C、 D、9. 如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是( )
A、 B、 C、 D、9. 如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是( )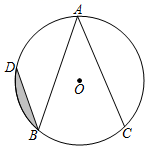 A、 ﹣ B、 ﹣ C、 ﹣ D、 ﹣10. 如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是( )
A、 ﹣ B、 ﹣ C、 ﹣ D、 ﹣10. 如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
 12. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.13. 小蕾有某文学名著上、中、下各1册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率是 .14. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为.
12. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.13. 小蕾有某文学名著上、中、下各1册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率是 .14. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为.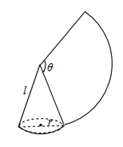 15. 如图,抛物线 (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线 与直线 有且只有一个交点;②若点 、点 、点 在该函数图象上,则 ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为 ;④点A关于直线 的对称点为C,点D、E分别在x轴和y轴上,当 时,四边形BCDE周长的最小值为 .其中正确判断的序号是
15. 如图,抛物线 (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线 与直线 有且只有一个交点;②若点 、点 、点 在该函数图象上,则 ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为 ;④点A关于直线 的对称点为C,点D、E分别在x轴和y轴上,当 时,四边形BCDE周长的最小值为 .其中正确判断的序号是
三、解答题
-
16. 先化简,再求值: ,其中x满足x2-3x+2=0.17. 为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.(1)、求这两年藏书的年均增长率;(2)、经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?18. 如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
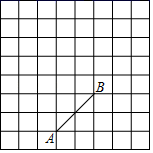 (1)、将线段AB向上平移两个单位长度,点A的对应点为点 ,点B的对应点为点 ,请画出平移后的线段 ;(2)、将线段 绕点 按逆时针方向旋转 ,点 的对应点为点 ,请画出旋转后的线段 ;(3)、连接 、 ,求 的面积.19. 某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。(1)、如果小芳只有一次摸球机会,那么小芳获得奖品的概率为;(2)、如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)20. 如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)、将线段AB向上平移两个单位长度,点A的对应点为点 ,点B的对应点为点 ,请画出平移后的线段 ;(2)、将线段 绕点 按逆时针方向旋转 ,点 的对应点为点 ,请画出旋转后的线段 ;(3)、连接 、 ,求 的面积.19. 某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。(1)、如果小芳只有一次摸球机会,那么小芳获得奖品的概率为;(2)、如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)20. 如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m. (1)、足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)、若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
(1)、足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)、若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
21. 图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.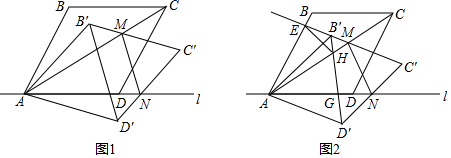 (1)、当MN∥B′D′时,求α的大小.(2)、如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.22. 如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)、当MN∥B′D′时,求α的大小.(2)、如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.22. 如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.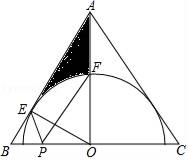 (1)、求证:AC是⊙O的切线;(2)、若点F是OA的中点,OE=3,求图中阴影部分的面积;(3)、在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.23. 在平面直角坐标系xOy中(如图).已知抛物线y=﹣ x2+bx+c经过点A(﹣1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)、求证:AC是⊙O的切线;(2)、若点F是OA的中点,OE=3,求图中阴影部分的面积;(3)、在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.23. 在平面直角坐标系xOy中(如图).已知抛物线y=﹣ x2+bx+c经过点A(﹣1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处. (1)、求这条抛物线的表达式;
(1)、求这条抛物线的表达式;
(2)、求线段CD的长;(3)、将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.