河北省新乐市2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2021-02-03 类型:期中考试
一、单选题
-
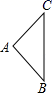
1. 规定:(→2)表示向右移动2记作+2,则(←3)表示向左移动3记作( )A、+3 B、﹣3 C、﹣ D、+2. 三角形ABC绕BC旋转一周得到的几何体为( )
 A、
A、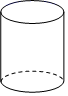 B、
B、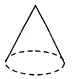 C、
C、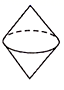 D、
D、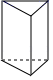 3. 把 写成省略括号的和的形式是( ).A、 B、 C、 D、4. 下列各组数中,结果一定相等的为( )A、 与 B、 与 C、 与 D、 与5. 如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )
3. 把 写成省略括号的和的形式是( ).A、 B、 C、 D、4. 下列各组数中,结果一定相等的为( )A、 与 B、 与 C、 与 D、 与5. 如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )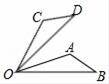 A、15° B、45° C、60° D、75°6. 若x=|﹣3|,|y|=2,则x﹣2y=( )A、﹣7 B、﹣1 C、﹣7或1 D、7或﹣17. 数 在数轴上对应的点如图所示,则 , , 的大小关系是( )
A、15° B、45° C、60° D、75°6. 若x=|﹣3|,|y|=2,则x﹣2y=( )A、﹣7 B、﹣1 C、﹣7或1 D、7或﹣17. 数 在数轴上对应的点如图所示,则 , , 的大小关系是( )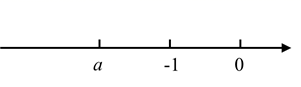 A、 B、 C、 D、8. 若∠α+∠θ=90°,∠β=∠θ,则∠α与∠β的关系是( )A、∠α与∠β互余 B、∠α与∠β互补 C、∠α与∠β相等 D、∠α大于∠β9. 有理数 在数轴上的位置如图所示,则下列结论正确的是( )
A、 B、 C、 D、8. 若∠α+∠θ=90°,∠β=∠θ,则∠α与∠β的关系是( )A、∠α与∠β互余 B、∠α与∠β互补 C、∠α与∠β相等 D、∠α大于∠β9. 有理数 在数轴上的位置如图所示,则下列结论正确的是( )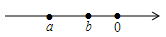 A、 B、 C、 D、10. 下列语句中,正确的个数是( )
A、 B、 C、 D、10. 下列语句中,正确的个数是( )①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.
A、1个 B、2个 C、3个 D、4个11. 若a+b<0,ab<0,则( )A、a>0,b>0 B、a<0,b<0 C、a,b两数一正一负,且正数的绝对值大于负数的绝对值 D、a,b两数一正一负,且负数的绝对值大于正数的绝对值12. 在如图所示的方格纸(1格长为1个单位长度)中, 的顶点都在格点上,将 绕点O按顺时针方向旋转得到 使各顶点仍在格点上,则其旋转角的度数是( )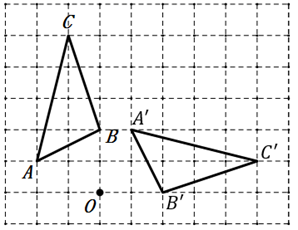 A、 B、 C、 D、13. 下列说法中,错误的是( )A、若点C在线段BA的延长线上,则BA=AC-BC B、若点C在线段AB上,则AB=AC+BC C、若AC+BC>AB , 则点C一定在线段BA外 D、若A , B , C三点不在同一条直线上,则AB<AC+BC14. 如图,点D把线段AB从左至右依次分成1∶2两部分,点C是AB的中点,若 ,则线段AB的长是( )
A、 B、 C、 D、13. 下列说法中,错误的是( )A、若点C在线段BA的延长线上,则BA=AC-BC B、若点C在线段AB上,则AB=AC+BC C、若AC+BC>AB , 则点C一定在线段BA外 D、若A , B , C三点不在同一条直线上,则AB<AC+BC14. 如图,点D把线段AB从左至右依次分成1∶2两部分,点C是AB的中点,若 ,则线段AB的长是( )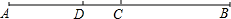 A、18 B、12 C、16 D、14
A、18 B、12 C、16 D、14二、填空题
-
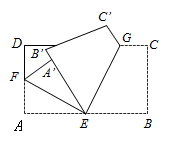
15. 若a,b互为相反数,则a2﹣b2= .16. =°.17. 若 、 为实数,且满足 ,则 .18. 一个角的补角与它的余角的3倍的差是40°,则这个角为 .19. 如图,将长方形 纸片按如图所示的方式折叠, 为折痕,点 落在 ,点 落在 点 在同一直线上,则 度;
三、解答题
-
20. 计算:(1)、(2)、21. 如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD的度数.结合图形,完成填空:

解:因为∠AOC+∠COB=°,
∠COB+∠BOD= ①
所以∠AOC= . ②
因为∠AOC=40°,
所以∠BOD=°.
在上面①到②的推导过程中,理由依据是: .
22. 如图,已知 ,求 的度数.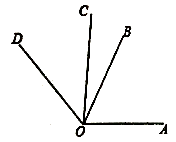 23. 快递配送员王叔叔一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,某天他从出发点开始所行走的路程记录为(长度单位:千米):+3,﹣4,+2.+3.﹣1,﹣1,﹣3(1)、这天送完最后一个快递时,王叔叔在出发点的什么方向,距离是多少?(2)、如果王叔叔送完快递后,需立即返回出发点,那么他这天送快递(含返回)共耗油多少升(已知每千米耗油0.2升)?24. 在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
23. 快递配送员王叔叔一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,某天他从出发点开始所行走的路程记录为(长度单位:千米):+3,﹣4,+2.+3.﹣1,﹣1,﹣3(1)、这天送完最后一个快递时,王叔叔在出发点的什么方向,距离是多少?(2)、如果王叔叔送完快递后,需立即返回出发点,那么他这天送快递(含返回)共耗油多少升(已知每千米耗油0.2升)?24. 在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.(提出问题)三个有理数a、b、c满足 ,求 的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即 , , 时,
则: ;
②当a,b,c有一个为正数,另两个为负数时,设 , ,
则:
所以: 的值为3或-1.
(探究)请根据上面的解题思路解答下面的问题:
(1)、三个有理数a,b,c满足 ,求 的值;(2)、已知 , ,且 ,求 的值.25. 如图,点C在线段AB上,M、N分别是线段AC、BC的中点, (1)、若AC=7cm,BC=5cm,求线段MN的长;(2)、若AB=a,点C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;(3)、若将(2)中“点C为线段AB上任意一点”改为“点C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.
(1)、若AC=7cm,BC=5cm,求线段MN的长;(2)、若AB=a,点C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;(3)、若将(2)中“点C为线段AB上任意一点”改为“点C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.